Bonjour ,
j'ai une exercice à résoudre mais je bloque ...
On considère le problème
min 2x1+9x2+3x3
sc : -2x1+2x2+x3>=1
x1+x2-x3>=1
x1,x2,x3>=0
1) résoudre graphiquement le dual
2) donner la solution du primal
3) quelle est la valeur optimale ?
Comme dual j'ai max (y1+y2)
sc
-2y1+y2<=2
2y1+4y2<=9
y1-y2<=3
y1,y2>=0
Dans la représentation graphique , je n'ai pas un polyèdre ...du coup j'ai pas les bons points pour résoudre le dual .
La troisième équation ne coupe les deux autres ...
Représentation graphique dual
12 messages
- Page 1 sur 1
Donc j'ai finalement comme solution optimale le point p3 avec comme valeur optimale 27/4 ?
Pour trouver la solution du primal , faut faire pour chaque cas , c'est à dire avec chaque sommet ?
Pour le 2e point j'ai comme solution du primal : (0,0,-1)
Le 3e :j'ai comme solution (1/4,3/4,0)
Le4e : j'ai un problème je trouve x2=-1/2 et x2=1 ...
Le 5e : (0,0,1)
ensuiite pour la valeur optimale , est ce qu'il faut remplacer ces solutions dans la fonction objectif du dual et regarder la plus élevée ?
Pour trouver la solution du primal , faut faire pour chaque cas , c'est à dire avec chaque sommet ?
Pour le 2e point j'ai comme solution du primal : (0,0,-1)
Le 3e :j'ai comme solution (1/4,3/4,0)
Le4e : j'ai un problème je trouve x2=-1/2 et x2=1 ...
Le 5e : (0,0,1)
ensuiite pour la valeur optimale , est ce qu'il faut remplacer ces solutions dans la fonction objectif du dual et regarder la plus élevée ?
J'ai rien compris à ce que tu as marquer :p Tu essayes de résoudre par le simplexe ?
Je pense qu'on veux te faire résoudre en utilisant le TEC :
[CENTER] [/CENTER]
[/CENTER]
Pour notre problème on a :
[CENTER]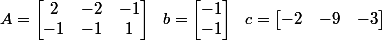 [/CENTER]
[/CENTER]
La solution optimale du dual est donnée sur mon graphique plus haut :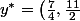) pour
pour 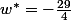 .
.
On résout alors le système :
[CENTER] y_1^* & = & 0 \\ \left (- x_1^* - x_2^* + x_3^* + 1 \right ) y_2^* & = & 0 \\ \\ \left ( 2 y_1^* - y_2^* + 2 \right ) x_1^* & = & 0 \\ \left (- 2 y_1^* - y_2^* + 9 \right ) x_2^* & = & 0 \\ \left (- y_1^* + y_2^* + 3 \right ) x_3^* & = & 0 \end{array}\right.) [/CENTER]
[/CENTER]
On obtient alors la solution :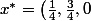) . On a bien
. On a bien 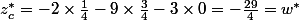 (dualité forte).
(dualité forte).
Et pour finir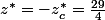
Je pense qu'on veux te faire résoudre en utilisant le TEC :
[CENTER]
 [/CENTER]
[/CENTER]Pour notre problème on a :
[CENTER]
La solution optimale du dual est donnée sur mon graphique plus haut :
On résout alors le système :
[CENTER]
On obtient alors la solution :
Et pour finir
Oui je me disais aussi , car cette méthode je ne sais pas si tout le monde l'a faite . Mais on nous a appris la méthode des écarts complémentaires .
On avait au départ la solution obtenue par le graphique (on avait plusieurs solutions) ou le simplexe .
Donc j'ai bien trouvé 29/4 pour la résolution graphique de la question a)
et donc la solution c'est (7/4,11/2)
Ensuite avec chaque point , c'est à dire les points du graphique , on appliquait la méthode des écarts complémentaires pour avoir la solution du primal . C'est ce que j'ai écrit dans le post précédent .
Donc la solution du primal c'est -29/4?
Je comprends pas , ça fonctionne avec ce que je fais ^^
En fait on faisait b-Ax comme tu as dit . et x en fait c'est chaque point trouvé à la question 1...
Edit : oui donc obtient la solution x=(1/4,3/4,0)!!
En fait je pense que je me suis cassé la tête à faire avec tous les points , mais fallait faire qu'avec la solution obtenue avant c'est à dire (7/4,11/2) ...
Par contre j'ai 29/4 en solution du dual , au lieu de -29/4 . Est ce dû au fait que moi en dual j'ai max et toi -min ? Normalement on devrait avoir la même chose non ?
On avait au départ la solution obtenue par le graphique (on avait plusieurs solutions) ou le simplexe .
Donc j'ai bien trouvé 29/4 pour la résolution graphique de la question a)
et donc la solution c'est (7/4,11/2)
Ensuite avec chaque point , c'est à dire les points du graphique , on appliquait la méthode des écarts complémentaires pour avoir la solution du primal . C'est ce que j'ai écrit dans le post précédent .
Donc la solution du primal c'est -29/4?
Je comprends pas , ça fonctionne avec ce que je fais ^^
En fait on faisait b-Ax comme tu as dit . et x en fait c'est chaque point trouvé à la question 1...
Edit : oui donc obtient la solution x=(1/4,3/4,0)!!
En fait je pense que je me suis cassé la tête à faire avec tous les points , mais fallait faire qu'avec la solution obtenue avant c'est à dire (7/4,11/2) ...
Par contre j'ai 29/4 en solution du dual , au lieu de -29/4 . Est ce dû au fait que moi en dual j'ai max et toi -min ? Normalement on devrait avoir la même chose non ?
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 [/CENTER]
[/CENTER]