Relation de bézout et congruence

[vivelesmaths75]

Bonsoir,

J'ai une petite question sur une proposition de correction que je ne saisis pas :

Sur la question suivante : "La comète A passe tous les 5 ans et a été observée l’année dernière. La comète B
passe tous les 8 ans et a ́ été observée il y a deux ans. Quelle est la prochaine fois où l’on pourra
observer les deux comètes la même année ?"

Une proposition de correction est : "On peut aussi écrire une relation de Bézout 2·8−3·5 = 1 et obtenir n ≡ (−1)·2·8+(−2)·(−3)·5 ≡−1 + ((−1) · 3 + (−2) · (−3)) · 5 ≡ −1 + 3 · 5 = 14 (mod 40)."

Je vois mal le passage de la retion de Bézout à la congruence de n même si je trouve pas ça déconnant, je ne trouve pas de théorème dans mon cours ni une claire compréhension de ma part qui nous permet de faire cela ... (je pense relié au pgcd et ppcm...).

Merci d'avance,

Yann

[GaBuZoMeu]

Bonsoir,
Il s'agit des restes chinois, on trouve un entier congru à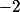 modulo 8 et à modulo 5, et plus précisément le plus petit entier positif satisfaisant ces congruences.
On observera les deux comètes la même année dans 14 ans, 54 ans, 94 ans ...
N'as-tu pas le théorème des restes chinois dans ton cours, et l'explication de l'algorithme basé sur une relation de Bézout ?

[vivelesmaths75]

Si j'ai effectivement les 2 ... Je vais retravailler tout cela... Merci pour votre aide!

[GaBuZoMeu]

Avec plaisir.