Réduction de matrices

[vejitoblue]

Hello



voilà on a cette matrice, on veut montrer qu'elle est diagonalisable , trouver une matrice de passage et calculer M^k (k entier)

bon j'ai calculé le polynome caractéristique ( disons chi(X)), je trouve X^4-13X^2+36, on a une racine un peu 'visible' en 2 on fait la division euclidienne de chi(X) par X-2 etc on trouve un polynome scindé à racines simples: chi(X)= (X-2)(X+2)(X-3)(X+3), on conclut que M est diagonalisable.
les valeurs propres sont {-2,-3,2,3} et avec un bref calcul, on a nos vecteurs propres, v(-2)= v(-3)= v(2)= v(3)=.

next, à priori M^k= PD^kQ avec D la matrice diagonale de valeurs propres et Q l'inverse de P (qui est la matrice de passage dans la base de vecteur propres), ce qui permet de calculer plus intelligement M^k que le brut calcul de MM.....M k fois.

Ma question c'est le calcul de Q (obligatoire si l'on veut calculer M^k) une matrice 4x4 ça fait quand même pas mal d'équations à résoudre, c'est laborieux en plus je suis un peu nul en calcul mental (thank god l'algèbre linéaire m'aide beaucoup), sans compter sur toute les erreurs qu'on peut faire. je demande pas une formule miracle (si compter qu'elle existe) mais comment peut-on se débrouiller de manière plus pragmatique.

(l'algèbre linéaire ça va pour moi jusqu'à ce qu'on me parle des matrices et surtout des déterminants, en gros ça va pas du tout lol)

[Ben314]

Salut,
Tu connais le théorème dit "de Cayley-Hamilton" ?

[Lostounet]

Salut

Fais la division euclidienne de X^n par chi(X).
Puis évalue la relation en M et utilise le fait que chi(M)=0 (Cayley Hamilton)

Edit désolé Ben grillé

[vejitoblue]

salut lostounet et ben
désolé j'ai pas les compétences pour comprendre où vous voulez en venir.
dans mon cours j'ai un vague théorème de calyley hamiton :
E de dim finie alors chi(M)=0 (ou encore chi(endomorphisme de M)=0) avec une preuve de ouf que j'ai pas encore pigé.

déjà chi(M) comment on le prononce, dans notre cas ça voudrait dire que M^4-13M^2 + 36I_4=0 (je mets tout à plat de chez plat pour mieux comprendre, chi(M) est donc une matrice)

lostounet c'est quoi le X^n que tu as mentionné

je réfléchis à tout ça merci

(j'essaye d"expliciter Q avec la relation PD^4Q-13PD^2Q+36I=0 des fois que.....)

[Lostounet]

En fait, suppose que je veuilles calculer M^6.

Je considère le polynôme P(X)=X^6
Et j'effectue sa division euclidienne par le polynôme chi(X) (lire "ki" pas "chie").

Donc par le théorème de division euclidienne, comme chi est de degré 4, il existe un polynôme Q(X) et un autre R(X) de degré au plus 3 tel que
(Relation ***)
X^6 = chi(X)*Q(X) + R(X)

Or R(X) est de la forme aX^3+bX^2+cX+d

Maintenant il suffit d'évaluer la relation (***) en les 4 valeurs qui annulent chi(X): tu trouveras alors les coefficients a b c et d explicitement en posant un petit système.

Pour finir, il suffit d'évaluer (***) en X=M.
Par le théorème de Cayley Hamilton, chi(M)=0 ce qui te donnera M^6 = R(M) = aM^3+bM^2 + cM + d

La même méthode marche pour toute puissance de M

[vejitoblue]

ok cimer, pas besoin d'expliciter Q dans ces conditions vu qu'en évaluant en M chi(M)Q(M) sera forcément nul (intégrité ce gerne de truc), je vais faire les calculs pour déjà m'accoutumer à cette idée =)

EN fait c'est sympa ce cayley hamilton, j'étais en train de me dire que ça sert à que dalle et boom une petite application.

++

[Lostounet]

Pas besoin d'expliciter Q en effet.

Mais pas lié à l'intégrité :p
À la limite le fait que M commute avec ses itérées.

[vejitoblue]

salut!
alors aujourd'hui je me suis attaqué à la réduction de jordan dunford chevalley:

d'après ce que j'ai compris dès qu'on est en dimension finie (j'imagine même pas les matrices en dim infini lol) et que le polynome caractéristique d'un endomorphisme est scindé, on peut tout le temps mettre cet endomorphisme sous forme d+n d diagonal et n nilpotent qui commutent (pour *)

osef pour l'instant de la théorie (j'ai zieuté vite fait la preuve à pas l'air si insurmontable), je cherche la pratique car bientôt exam etc on aura surement un exo là dessus.

mon exemple donc:


la méthode que j'ai c'est calculer le polynome caractéristique, trouver une base des sous espaces propres, la completer (au cas où, j'imagine, la multiplicité algébrique est différente de la mult géométrique), calculer la matrice de passage P et son inverse Q, et enfin on explicite la matrice diagonale et la matrice nilpotente.

donc chi(X)=X(X-1)² l'espace propre associé à 0 , E_o=vect(1,-1,-1), pour E_1 a priori il est engendré par un seul vecteur style (1,0,-1) (on peut pas jouer avec le système d'équation plus que ça) donc on le complète avec un vecteur pour former une base de R² ex: (-1,1,0).

On a donc la matrice de passage

on déduit son inverse:


ensuite


voila j'ai plus qu'à dire que la matrice diagonale est et que la matrice nilpotente est

N²=0 et DN=ND (commutativité) du coup on a décomposé A en dunford style.

et ce truc ça marche toujours sous les hypothèse, c'est toujours si simple Enfin le truc qui me chiffonne c'est que je fais des calculs qui me dépassent complétement, demain je fais un peu de théorie, faire des choses qu'on comprend pas c'est chaud

(je transforme ce fil en journal intime wesh)

[Ben314]

. . . donc on le complète avec un vecteur pour former une base de R² ex: (-1,1,0). . .
. . . voila j'ai plus qu'à dire que la matrice diagonale est et que la matrice nilpotente est

NON : Si tu choisi le troisième vecteur "au pif" (comme tu semble le faire), il n'y a aucune raison particulière que ta matrice nilpotente soit de cette forme là :
Comme , ça signifie que ta base {e1,e2,e3} est telle que f(e1)=0; f(e2)=e2 (jusque là, O.K. vu que tu as pris pour e1 et e2 des vecteurs propres) mais aussi que tu as f(e3)=e2+e3 et ça, si tu choisi e3 au pif, il n'y a aucune raison que ce soit vrai.

[vejitoblue]

salouté ben.

je comprends pas tout, alors on me dit de compléter en un base je complète. je vois pas pourquoi prendre un vecteur spécifique, (si on prend un vecteur de ker(A-I) il sera lié et on aura pas une base de R^3). en gros on change de base et on a une matrice qui est semblable à A, elle rep le même endomorphisme il me semble. donc tant qu'on peut choisir une base dans laquelle notre endomorphisme est le plus facile à étudier possible on le fait.

sinon j'ai cru comprendre aussi que la décomposition de dunford est unique. J'ai peut-être eu de la chance ce coup-ci et si on prend un vecteur de completage au pif ce sera pas si évident à chaque fois.

Sinon comment réduit on en dunford-jordan J'ai lu qu'il y a quelques méthodes comme en s'appuyant sur l'arithmétique de K[X] et le lemme des noyaux ou encore la méthode de Newton (je ne vois même pas le rapport pour l'instant, juste 'feuilleter' quelques pdf sur le net)

++

[vejitoblue]

hello!
j'ai essayé une réduction avec les projecteurs spectraux.


il vaut aussi le polynome minimal
(X-1)² est (X+2) sont premiers entre eux (division euclidienne, barbare)
donc bezout => A B K[X] A(X-1)²+B(x+2)=1

après on fait la petite DES de 1/chi(X) histoire d' aboutir à un endo sous la forme de somme de projecteurs spectraux (et lemme des noyaux => d diagonalisable enfin plus ou moins l'idée que j'ai capté)

j'ai trouvé que 1 =(x-1)² + (x+2)(x-2)
c'est maintenant que le bas baisse sic

En évaluant en A (vu que les projecteur sont des polynomes d'endomorphisme), j'arrive à une matrice zarbi

D=

impossible de voir "immédiatement qu'elle est diagonalisable et encore moins que N=A-D est nilpotente
Donc je dois encore diagonailiser D et refaire encore des calculs

c'est énervant alors que cette fois si je comprend un peu mieux ce que je fais que dans le dernier message (mais c'est pas encore super clair), j'ai vérifie plusieurs fois les calculs même en ajoutant les valeurs propre et tout j'ai loupé un truc

[vejitoblue]

. . . donc on le complète avec un vecteur pour former une base de R² ex: (-1,1,0). . .
. . . voila j'ai plus qu'à dire que la matrice diagonale est et que la matrice nilpotente est

NON : Si tu choisi le troisième vecteur "au pif" (comme tu semble le faire), il n'y a aucune raison particulière que ta matrice nilpotente soit de cette forme là :
Comme , ça signifie que ta base {e1,e2,e3} est telle que f(e1)=0; f(e2)=e2 (jusque là, O.K. vu que tu as pris pour e1 et e2 des vecteurs propres) mais aussi que tu as f(e3)=e2+e3 et ça, si tu choisi e3 au pif, il n'y a aucune raison que ce soit vrai.

j'ai perdu mon sauveur

j'ai recommencé l'exo en faisant tout bien, je te (vous) explique
donc j'ai cherché une base du sous espace caracteristique (ker ((A-I)²)) j'ai donc cette fois ci une base de R^3 composé uniquement de vecteurs propres ((0,1,-1) et (1,0,-1) pour E1 et (-1,1,1) pour E0) , j'ai donc traduit la matrice A dans cette base et j'ai trouvé:



qu'on décompose en dunford (j'ai pas vérifié que D et N commutent mais N^3=0). c'est encore de la sorcellerie mais je continue d'apprendre

si c'est bon j'ai fait ma première décomposition ++

[Pseuda]

Bonjour,

Je vais essayer de t'aider en rassemblant mes souvenirs. Cela ne me parait pas bon car :
- les sous-espaces caractéristiques doivent être stables pour l'endomorphisme associé à la matrice A (et là ce n'est pas le cas car f(e1)=e1-2e3 avec e3 qui appartient au sous-espace associé à 0)
- la matrice nilpotente doit l'être en 2 coups car on a du ker(A-I)^2.

Sans garantie aucune. J'espère que quelqu'un passera par là.

[vejitoblue]

salut pseuda!

IMPOSSIBLEUH OUINNN!! ça fait deux jours que j'essaye et je pensais enfin...

donc comme les deux sous espaces sont en somme directe, il sont supplémentaires et on devrait avoir des zéros partout sur la 3eme lignes (y compris la derniere vu qu'on veut une diagonale de valeurs propres) c'est ça

la matrice nilpotente doit l'être en duex coups ça veut dire qu'on doit la multiplier deux fois pour avoir la nullité

[vejitoblue]

laisse tomber j'ai du me tromper dans l'inverse de la matrice de passage j'ai pas PQ=I

[vejitoblue]

j'ai ça ça devrait le faire:



là on est bien on a f(e3)=e3 du coup on a la stabilité partout

il reste plus qu'à décomposer en PAQ= D+N=

fiouuuuuuuuuuu mais que c'est relou (et encore j'ai pas vérifier la nilpotence et tout gare au surprise le 1 en position 33 a l'air de jamais s'annuler)

[Ben314]

donc j'ai cherché une base du sous espace caracteristique (ker ((A-I)²)) j'ai donc cette fois ci une base de R^3 composé uniquement de vecteurs propres ((0,1,-1) et (1,0,-1) pour E1 et (-1,1,1) pour E0) , j'ai donc traduit la matrice A dans cette base et j'ai trouvé:

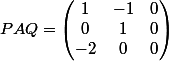
J'ai pas trop compris ce que tu foutait, ni quelle était la matrice A avec laquelle tu voulais faire tes essais.

Mettons que ta matrice A soit 3x3 et que le polynôme caractéristique soit P(X)=(X-m)(X-1)^2.

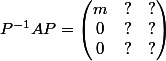
- Concernant la valeur propre m, tu es sûr d'avance que le sous espace propre ker(A-m.I3) est de dimension 1 et tu peut via des calculs en trouver une base formée d'un unique vecteur E1 et sans même connaitre les deux autres vecteurs que tu va choisir pour ta base, tu sait que la matrice de A dans une base {E1,?,?} ça va être de la forme (1)
- Concernant la valeur propre 1, le sous espace propre ker(A-I3) est de dimension 1 ou 2 et la matrice est diagonalisable ssi c'est de dimension 2. il y a plusieurs façon de savoir à quoi s'en tenir : soit on cherche les vecteurs propres, c'est à dire qu'on résous le système (A-I3).X=0 et on voit bien si c'est de dim 1 ou 2, soit on
cherche le polynôme minimal de A qui ne peut être que (X-m)(X-1) ou bien (X-m)(X-1)^2 et pour savoir lequel des deux c'est, il suffit de calculer (A-m.I3)(A-I3) et de regarder si ça fait la matrice nulle ou pas.
Si jamais ce que tu as fait, c'est de chercher les valeurs propres et que, pas de bol, ça fait un s.e.v. que de dim 1, donc un unique vecteur E2, alors il te manque effectivement le 3em vecteur, mais tu sait déjà parfaitement bien que dans ta (future) base {E1,E2,?} la matrice de l'endomorphisme sera de la forme
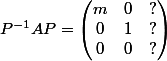
(1)
Concernant le choix de E3, il y a évidement plusieurs possibilité pour trouver un truc "simple".
a) Tu peut effectivement évaluer le sous espace caractéristique ker((A-I3)^2) qui lui sera forcément de dim 2 et qui, bien sûr va contenir le s.e.v. propre ker(A-I3) donc contenir E2. Donc tu va pouvoir choisir E3 tel que {E2,E3} soit une base de ker((A-I3)^2) et ça te garanti que dans la base {E1,E2,E3} la matrice de l'endomorphisme sera de la forme
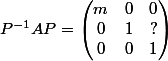
(1)
Et, quitte à multiplier E3 par une constante, on peut se débrouiller pour que ?=1
b) L'autre solution, ça consiste à utiliser la théorie qui est sensée être connue qui te dit qu'il est possible de choisir E3 tel que dans la base {E1,E2,E3} la matrice de l'endomorphisme soit de la forme

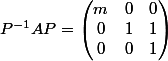
Et ça te dit qu'on peut trouver E3 tel que A.E3=E2+E3, c'est à dire (A-I3).E3=E2.
Et comme tu connait déjà E2, ben t'a juste à résoudre ce système et à prendre pour E3 une des multiples solutions.

(1) Et c'est là que je comprend que dalle à ce que tu as fait vu que la seule matrice que tu as écrit, ben ça a pas du tout cette tête là...

[vejitoblue]

t'es un mac merci!! j'ai absolument tout compris. (t'as ouvert des portes que je n'arrivais pas à enfoncer)

ps: ah ouais le zgen il m'a mis high

[Pseuda]

j'ai ça ça devrait le faire:



là on est bien on a f(e3)=e3 du coup on a la stabilité partout

il reste plus qu'à décomposer en PAQ= D+N=

fiouuuuuuuuuuu mais que c'est relou (et encore j'ai pas vérifier la nilpotence et tout gare au surprise le 1 en position 33 a l'air de jamais s'annuler)

Cela ne me paraît pas aller encore, désolée, car les éléments diagonaux de la matrice PAQ (que des 1) ne correspondent pas aux valeurs propres (des 0 et des 1) que tu as trouvées. Et la matrice N n'est pas nilpotente non plus car on a u(e3)=e3 ad vitam aeternam...

[vejitoblue]

ouais merci, j'ai compris des trucs grâce à vous deux
je devrais avoir une matrice semblable avec les vp sur la diagonale. j'avais du mal à me représenter un endomorphisme sur une matrice et maintenant ça commence à devenir clair.

Maintenant fini les calculs foireux tete baissée, je saurais à quoi ressemble mes matrices et tout de suite si je vais dans le mur ou pas,

++