Réduction de Jordan

[kaya]

Salut à tous
Juste un ptit problème: je sais pas faire une réduction de Jordan
J'ai déjà plein de cours mais j'arrive pas trop à comprendre. Je demande de l'aide.
Ce serait sympa si vous me guidiez dans un site où je pourrais trouver des corrigés (avec toutes les démarches à suivre bien sur).
Sinon j'éssaie de réduire cette matrice en réduite de Jordan:



J'ai trouver:
-Polynôme caractéristique :
-Polynôme minimale :

Merci et A+

[Antho07]

Salut à tous
Juste un ptit problème: je sais pas faire une réduction de Jordan
J'ai déjà plein de cours mais j'arrive pas trop à comprendre. Je demande de l'aide.
Ce serait sympa si vous me guidiez dans un site où je pourrais trouver des corrigés (avec toutes les démarches à suivre bien sur).
Sinon j'éssaie de réduire cette matrice en réduite de Jordan:



J'ai trouver:
-Polynôme caractéristique :
-Polynôme minimale :

Merci et A+

Bon déja la diagonale sera (0,0,1,1).

Ensuite il faut regarder la multiplicité des valeurs propres dans le polynome MINIMAL.
Cela donne la taille des blocs de jordans associé à ces valeurs propres.
Ainsi les blocs de la valeur propre 0 sont de taille 1.
Celui de valeur propre 1 est de taille 2.

d'ou la réduite de Jordan est:




Cherches-tu aussi la matrice de passage?

(J'ai donné des justfications bancales, je reposterais dans la journée si j'ai le temps une méthode complète pour déterminer une réduite de jordan lorsque le polynome caracteristique est scindé)

[Antho07]

Bon alors le nombre de bloc de jordan associé a une valeur propre est la dimension du sous esapce propre associée.

La taille du grand bloc associée a une valeur propre est la multiplicité de cette valeur propre dans le polynome minimal

[Clembou]

Bon alors le nombre de bloc de jordan associé a une valeur propre est la dimension du sous esapce propre associée.

La taille du grand bloc associée a une valeur propre est la multiplicité de cette valeur propre dans le polynome minimal

Si il y a deux valeurs propres de multiplicité 2 et 1 pour une matrice alors la matrice n'est pas diagonalisable...

[Antho07]

Si il y a deux valeurs propres de multiplicité 2 et 1 pour une matrice alors la matrice n'est pas diagonalisable...

J'ai en effet du dire une grosse annerie dans mon premier post.

La forme de Jordan est plutot celle ci



La taille du plus grand bloc associé a la valeur propre est 1 (donc ya deux bloc car la somme des tailles doit faire 2).
En revanche il y a un bloc de taille 2 associée a la valeur propre 0.

[kaya]

Je vous remercie à tous pour vos réactions. Mais....
Le résultat est bien envisageable vu que le polynôme minimal est de degré 3.
le seul problème c'est comment avoir ce résultat. c'est surtout la démarche qui m'intéresse. En plus on nous dit toujours que dans un problème de réduction matricielle le résultat doit être un couple de matrice: la matrice réduite et la base où elle prend cette forme...n'est-ce pas?
Merci

[Antho07]

Je vous remercie à tous pour vos réactions. Mais....
Le résultat est bien envisageable vu que le polynôme minimal est de degré 3.
le seul problème c'est comment avoir ce résultat. c'est surtout la démarche qui m'intéresse. En plus on nous dit toujours que dans un problème de réduction matricielle le résultat doit être un couple de matrice: la matrice réduite et la base où elle prend cette forme...n'est-ce pas?
Merci

Tu cherche la matrice de passage donc??

[Antho07]

Pour la matrice de passage, on remarque ici que la restriction de ton endormorphime au sous espace caracteristique associé a la valeur propre 1 est diagonalisable(Le sous espace caracteristique est donc un sous espace propre).Les deux derniers vecteurs colonnes de ta matrice de passage forment une base de

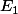
la restriction au sous-espace caracteristique associé à 0 n'est en revanche pas diagonalisable.

PAr conséquent il faut qu'on cherche deux vecteurs e1 et e2 tels que

u(e1)=0 u(e2)=e1 (pour etre de a forme voulu).


DOnc ici, si on prend un vecteur qui est dans ker(u²) mais pas dans ker(u).
PAr exemple e2=(0,0,0,1).
alors u(e2)=(0,0,-1,-1) est dans ker (u²).

Ainsi, (0,0,-1,-1) et (0,0,0,1) sont les deux premiers vecteurs de la matrice de passage. Ils forment une base de l'espace caracteristique associée à la valeur 0.

Completons avec une base de E1 et nous avons notre matrice de passage (les sous espaces caracteristiques sont en somme directe donc la famille sera libre donc on obtiendra bien une base).

PAr exemple les vecteurs (1,1,0,1) et (-1,-2,1,0) conviennent.


Finalement la matrice de passage suivante:



vérifient

[kaya]

Tu cherche la matrice de passage donc??

Exactement. Malheureusement je sais pas comment faire...
Vu le rapport entre et on peut déjà voir clairement qu'une partie de la matrice réduite

soit d'une forme diagonale dont les éléments de la diagonale sont {0,0,1,1} et le reste doit être égal à sauf (1ère ligne 2è col) qui devrait être égal à ou dans le cas général d'une forme "réduite de Jordan". alors qu'ici ne peut être égal à 0 sinon donc .
Mais la matrice de passage = :hein3: :hein3: :hein3:

[kaya]

Là c'est compris...
Merci infiniment pour vos réactions en particulier cette dernière explication de Antho07.
Je crois que ça pourra plus m'échapper.

[Antho07]

Là c'est compris...
Merci infiniment pour vos réactions en particulier cette dernière explication de Antho07.
Je crois que ça pourra plus m'échapper.

http://www.maths-forum.com/showthread.php?t=65534

J'ai tenté ici d'expliquer comment la jordanisation fonctionnait mais je n'ai pas tout démontré, la construction de cette base est quand meme assez fastidieuse