Récurrence multiple (et autres questions sur les suites)
63 messages
- Page 3 sur 4 - 1, 2, 3, 4
Je reviens sur un point précédent du même exo qui m'a incapacité :
Jusque-là, c'est bon, vient ensuite... :
Et là je bloque.
Merci pour toute suggestion.
Nous posons
Partie A :n'est jamais entier.
S'ensuivent plusieurs questions intermédiaires, où l'on cherche par récurrence à établir que "s'écrit sous la forme
".
On recontre un blocage lorsqueimpair. Il est donc suggéré de construire une récurrence forte afin de débloquer la situation :
"On suppose que pour un certain n supérieur à 2, les réelsjusqu'à
s'écrivent tous sous une forme
.
Si n est pair, on sait que l'on obtient la forme voulue.
Si n est impair, écrivons-le n=2m+1, m entier supérieur à 1.
Vérifier que
"
Jusque-là, c'est bon, vient ensuite... :
Vérifier que ceci s'écrit encore
Et là je bloque.
Merci pour toute suggestion.
Kikoo <3 Bieber a écrit:Une petite aide please ?
Je te confirme que mettre au même dénominateur marche pour montrer que 1+1/3+...+1/(2m+1) s'ecrit K/(2L+1) avec K et L des entiers naturels non nuls. On sait également en appliquant lhypothèse de récurrence au rang m+1 que
Il vient donc
Salut !
J'étudie les polynômes de Tchebychev de première espèce et je bloque sur une simple récurrence double.
La question :
L'initialisation ne pose pas de problème mais l'hérédité oui.
Je suppose que pour un certain n supérieur à 0, la propriété est vérifiée aux rangs n et n+1.
En utilisant l'hypothèse de récurrence, je me propose de montrer qu'elle est vraie au rang n+2.
Je tombe sur)=2\cos(\theta)\cos\((n+1) \theta\)-\cos\(n\theta\))
Mais comment arriver à \theta\)) ?
?
Merci pour votre aide !
J'étudie les polynômes de Tchebychev de première espèce et je bloque sur une simple récurrence double.
La question :
Pour x réel, on poseet
...
Montrer pour tout n entier naturel, pour tout theta réel que
L'initialisation ne pose pas de problème mais l'hérédité oui.
Je suppose que pour un certain n supérieur à 0, la propriété est vérifiée aux rangs n et n+1.
En utilisant l'hypothèse de récurrence, je me propose de montrer qu'elle est vraie au rang n+2.
Je tombe sur
Mais comment arriver à
Merci pour votre aide !
Ah non, c'est bon je viens d'y arriver :girl2:
J'expose mon calcul si jamais quelqu'un en a besoin :
Pour n=0, on a=1) et
et =1)
Pour n=1, on a=\cos(\theta\times 1)=\cos(\theta))
Supposons désormais pour n et n+1 tels que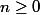 que :
que :
=\cos(n\theta)) et
et =\cos((n+1)\theta)) .
.
Montrons qu'au rang n+2 on a :
[CENTER]=\cos((n+2) \theta)=\cos((n+2) \theta)=\cos(n \theta)\cos(2 \theta)-\sin(n \theta)\sin(2 \theta)) [/CENTER]
[/CENTER]
On sait que :
=2\cos\theta T_{n+1}(\cos\theta)-T_n(\cos\theta) \\<br />\underbrace{=}_{HR} 2\cos\theta\,\cos((n+1) \theta)-\cos(n \theta) \\<br />=2\cos\theta\(\cos(n \theta)\cos\theta -\sin(n \theta)\sin\theta\)-\cos(n \theta) \\<br />=2\cos^2\theta\, \cos(n \theta)-\sin(2 \theta)\sin(n \theta)-\cos(n \theta))
Or :
-\cos(n \theta) \\<br />=\cos(n \theta)(2\cos^2\theta -1) \\<br />=\cos(n \theta)\cos(2 \theta))
Donc finalement nous aboutissons à la formule d'hypothèse.
Nous concluons la récurrence.
J'expose mon calcul si jamais quelqu'un en a besoin :
Pour n=0, on a
Pour n=1, on a
Supposons désormais pour n et n+1 tels que
Montrons qu'au rang n+2 on a :
[CENTER]
On sait que :
Or :
Donc finalement nous aboutissons à la formule d'hypothèse.
Nous concluons la récurrence.
Ca me fait bizarre de répondre à mes propres questions... :ptdr:
J'écris et j'espère que quelqu'un passera pour me dire si ce que j'ai fait est juste, j'ai pas envie de me planter tout seul.
 , Il me faut montrer que
, Il me faut montrer que  est une fonction polynômiale.
est une fonction polynômiale.
Cela revient à ce que je prouve que s'écrit sous la forme :
s'écrit sous la forme :
=a_nX^n+a_{n-1}X^{n-1}+...+a_1X+a_0)
Or je sais que=\cos(n\theta))
Il faut alors désormais exhiber) comme étant une somme de monômes en
comme étant une somme de monômes en 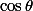 .
.
Or :
=\Re \((\cos\theta+i\sin\theta)^n\) \\<br />=\Re\(\sum_{k=0}^n{n\choose k}\cos^k\theta+i^{n-k}\sin^{n-k}\theta\))
J'écris et j'espère que quelqu'un passera pour me dire si ce que j'ai fait est juste, j'ai pas envie de me planter tout seul.
Cela revient à ce que je prouve que
Or je sais que
Il faut alors désormais exhiber
Or :
Kikoo <3 Bieber a écrit:Ca me fait bizarre de répondre à mes propres questions... :ptdr:
J'écris et j'espère que quelqu'un passera pour me dire si ce que j'ai fait est juste, j'ai pas envie de me planter tout seul., Il me faut montrer que
est une fonction polynômiale.
Cela revient à ce que je prouve ques'écrit sous la forme :
Or je sais que
Il faut alors désormais exhibercomme étant une somme de monômes en
.
Or :
Et là, quand tu passes à la partie réelle certains termes de la somme vont s'en aller (lesquels), ensuite un changement d'indice, un petit remplacement à coup de cos^2+sin^2=1 et c'est gagné.
Cette formule a le mérite d'exister, mais si l'on veut utiliser les polynômes de Tchebychev il est plus rapide d'implémenter un algorithme de calcul à partir de la formule de récurrence.
Sinon on aurait aussi pu montrer que Tn est un polynôme (c'est un polynôme, pas une fonction polynomiale. Bon la différence n'est pas flagrante à ce niveau, mais elle existe: ce ne sont pas des objets de même type) par récurrence sur n, en utilisant la formule de récurrence.
Kikoo <3 Bieber a écrit:Une petite question dans la foulée.
Comment appelle-t-on le processus inverse de la linéarisation ? Je cherche à exprimer un cos(kx) en un polynôme deet
...
J'avais lu dans un bouquin d'exos de TS un exercice comme celui-ci. Il s'appelait "processus inverse de la linéarisation". :we:
Le processus inverse de la linéarisation s'appelle donc "processus inverse de la linéarisation".
Kikoo <3 Bieber a écrit:Ah non, c'est bon je viens d'y arriver :girl2:
J'expose mon calcul si jamais quelqu'un en a besoin :
Pour n=0, on aet
Pour n=1, on a
Supposons désormais pour n et n+1 tels queque :
et
.
Montrons qu'au rang n+2 on a :
[CENTER][/CENTER]
On sait que :
Or :
Donc finalement nous aboutissons à la formule d'hypothèse.
Nous concluons la récurrence.
C'est bon, mais attention de bien séparer dans la rédaction ce que tu veux montrer de l'objet du calcul.
Notamment "Montrons que
et ensuite partir de
Alors que là, tu as commencé les calculs dans l'énoncé de ce que tu voulais montrer, ce qui induit le lecteur en erreur.
Pour rédiger la fin de l'hérédité, les mots sont "canoniques", il faut et il suffit d'écrire : "d'où l'hérédité. On conclut d'après le principe de récurrence que pour tout n ...." ou plus court "d'où l'hérédité. Ce qui clôt la récurrence." La deuxième fonctionne si tu as bien écrit explicitement l'hypothèse de récurrence.
Petites questions bonus sur les polynômes de Tchebychev (plutôt niveau spé que sup vers la fin) :
a) Montrer que le coefficient dominant de est
est 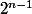 , pour
, pour 
On note désormais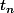 le polynôme
le polynôme  divisé par son coefficient dominant. Ainsi,
divisé par son coefficient dominant. Ainsi, 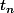 est unitaire.
est unitaire.
b) Justifier l'existence et calculer le sup de|) pour x dans l'intervalle [-1,1]
pour x dans l'intervalle [-1,1]
c) Trouver explicitement en quels points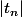 atteint son sup.
atteint son sup.
d) (facultatif) Tracer les graphes des fonctions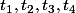 sur [-1,1]
sur [-1,1]
e) Soit P un polynôme unitaire de degré n, identifié ici à la fonction polynomiale, tel que le sup de |P(x)| sur [-1,1] soit strictement plus petit que le sup de |t_n| sur [-1,1]. En considérant=t_n(x)-P(x)) , arriver à une contradiction.
, arriver à une contradiction.
f) Application : Soit . On note
. On note 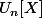 l'ensemble des polynômes unitaires de degré n. Encore une fois, on identifie polynôme et fonction polynomiale.
l'ensemble des polynômes unitaires de degré n. Encore une fois, on identifie polynôme et fonction polynomiale.
Déterminer|))
a) Montrer que le coefficient dominant de
On note désormais
b) Justifier l'existence et calculer le sup de
c) Trouver explicitement en quels points
d) (facultatif) Tracer les graphes des fonctions
e) Soit P un polynôme unitaire de degré n, identifié ici à la fonction polynomiale, tel que le sup de |P(x)| sur [-1,1] soit strictement plus petit que le sup de |t_n| sur [-1,1]. En considérant
f) Application : Soit
Déterminer
Salut ! 
J'ai) pour tout n positif définie par :
pour tout n positif définie par :
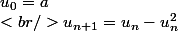
Il me faut montrer qu'il existe un tel que
tel que 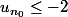 et que pour ce même entier, pour tout n qui lui est supérieur, on a
et que pour ce même entier, pour tout n qui lui est supérieur, on a ) .
.
Première partie, c'est immédiat vu que la suite diverge vers - l'infini (on utilise alors la définition d'une telle suite et on fixe un réel qui vaut -2).
Pour la deuxième partie, je veux faire une récurrence qui part de et l'hérédité aboutit mais pas l'initialisation...
et l'hérédité aboutit mais pas l'initialisation...
Merci pour l'aide que vous me fournirez
J'ai
Il me faut montrer qu'il existe un
Première partie, c'est immédiat vu que la suite diverge vers - l'infini (on utilise alors la définition d'une telle suite et on fixe un réel qui vaut -2).
Pour la deuxième partie, je veux faire une récurrence qui part de
Merci pour l'aide que vous me fournirez
Nightmare a écrit:Ah c'est bon, je l'ai retrouvé sur wikipédia, il ne s'agit pas de 2^n mais de 2n.
Le critère :
Si P(1) vraie
Si P(n) vraie => P(2n) vraie
Si P(n+1) vraie => P(n) vraie
Alors P(n) vraie pour tout n.
La preuve n'est pas inintéressante à travailler. Voyez-vous un bon exercice d'application de cette récurrence particulière?
Y a une preuve marrante de l'inégalité arithmético-geométrique qui l'utilise je crois.
63 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
