Recherche d'une formule de la somme des racines carrés consécutif
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Sep 2015, 16:04
par zygomatique » 16 Sep 2015, 16:04
salut
JFF ...posons
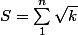
lorsqu'on sait que la fonction racine carrée est sous-additive (f(a + b) = \dfrac 1 2 n \sqrt {n + 1} \le S[/TEX]
d'autre part l'inégalité de Cauchy-Schwartz donne aussi (puisque tout nombre est multiple de 1) ::
}2} = \dfrac 1 {\sqrt 2} n \sqrt {n + 1})
donc au final ::
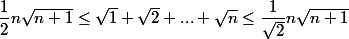
je ne sais pas s'il est plus mieux bien mieux meilleur que celui qui a déjà été proposé mais je le trouve très pas mal car c'est le mien de mon idée ... :ptdr:
la majoration par C-S est assez classique ... mais la minoration faut en avoir l'idée .... (enfin peut-être est-ce ainsi que cela est fait ...)
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Gloro
- Messages: 2
- Enregistré le: 16 Sep 2015, 13:59
-
 par Gloro » 18 Sep 2015, 17:00
par Gloro » 18 Sep 2015, 17:00
donald141 a écrit:Bonjour,
Je viens de terminer la démonstration de la somme des carrés consécutif : 1/6*n*(n+1)(2n+1) = 1² + 2² + 3² ... + n² .
Je suis a la recherche d'une formule pour calculé la somme des racines carrés consécutives : racine(1) + racine(2) + racine(3) + ... + racine ( n) .
Cela fais plusieurs jour que je cherche en utilisant comme piste la démonstration de la somme des carrés consécutif , sans aboutir et je n'ai pas trouvé d'aide sur internet.
Pourriez vous m'aider ? S'il vous plait.
Au revoir
Nouvelle formule trouvée dans un article récent pour la somme des racines carrées consécutives:
1/3.(racine((n + 1)^3) + racine(n^3) - 1).
Pour détails, lisez l'article en suivant le lien:
http://www.ahewar.org/eng/show.art.asp?t=0&userID=0&aid=2158
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
