[L1] rayon convergence du DS de tangente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 18 Oct 2008, 13:00
par mathelot » 18 Oct 2008, 13:00
Bjr,
Je ne sais comment calculer le rayon de convergence
du développement en série de la fonction tangente.
(DL de Taylor-Maclaurin)
merci d'avance.
PS: est ce qu'il suffit d'étudier
=\frac{\sin(x)}{1-(1-\cos(x))})
pour obtenir
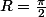
car 1-\cos(x)=o(1) au voisinage de zéro.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 18 Oct 2008, 16:00
par tize » 18 Oct 2008, 16:00
Salut mathelot :we:
Cela fait assez longtemps pour moi mais il me "semble" (à prendre avec de gros guillemets) qu'il y a un théorème d'analyse complexe qui dit un truc du genre : si f est DSE en 0 avec f(0) non nul alors 1/f est aussi DSE en 0 et le rayon de convergence de 1/f est inf(|z| ; z dans Z(f)) où Z(f) est l'ensemble des zéros de f...
Mais j'ai peut être rêvé tout ça...
-
mathelot
 par mathelot » 18 Oct 2008, 22:22
par mathelot » 18 Oct 2008, 22:22
Bonsoir,
voilà une démo que
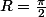
=\frac{\sin(x)}{\cos(x)}=\frac{\sin(x)}{1-(1-\cos(x))})
comme la série
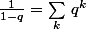
converge pour |q|<1
la série de tan converge simplement pour -1 < 1-cos(x) <1
ie sur
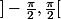
est-ce correct ?
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 19 Oct 2008, 08:09
par Maxmau » 19 Oct 2008, 08:09
Bj
Ta « preuve » me laisse tout à fait perplexe
Je reprends largumentation de tize de manière légèrement différente
La fonction tan(z) = sin(z)/cos(z) est holomorphe dans le disque ouvert de rayon ;)/2 centré en lorigine. Cela parce le zéro de cos(z) le plus proche de lorigine est ;)/2.
Elle est donc développable en série entière de rayon R >= ;)/2. Ce rayon ne saurait être > ;)/2 puisque ;)/2 est un pôle de tan(z).
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Oct 2008, 11:24
par tize » 19 Oct 2008, 11:24
Bonjour,
Pour Maxmau :
Je n'avais donc pas rêvé, aurais-tu une référence biblio de cette propriété s'il te plait, j'ai regardé dans mon vieux livre de prépa (Arnaudiès) sans rien trouver là dessus...
Pour Mathelot :
cela me semble possible oui,
=\frac{1}{1-z})
admet un DSE(0) avec un rayon de CV 1 et h(z)=1-cos(z) vaut 0 en 0 et admet un DSE(0)
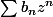
avec un rayon de CV infini, alors si
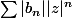
<1 pour
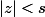
, f

h est DSE(0) avec un rayon de CV au moins égal s
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 19 Oct 2008, 18:12
par Maxmau » 19 Oct 2008, 18:12
tize a écrit:Bonjour,
Pour Maxmau :
Je n'avais donc pas rêvé, aurais-tu une référence biblio de cette propriété s'il te plait, j'ai regardé dans mon vieux livre de prépa (Arnaudiès) sans rien trouver là dessus...
Bonjour
D'une manière générale, dans tout cours (bouquin ou poly) de variable complexe.
A coup sûr, dans la vieille bible "théorie des fonctions" de Georges Valiron (chez Masson) .
Paragraphe 183: Formule fondamentale de cauchy, Existence de dérivées des fonctions holomorphes, série de Taylor
pages 367 ,368, 369
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 19 Oct 2008, 18:17
par tize » 19 Oct 2008, 18:17
Merci beaucoup pour la référence :we:
-
mathelot
 par mathelot » 20 Oct 2008, 07:34
par mathelot » 20 Oct 2008, 07:34
Maxmau a écrit:Ta « preuve » me laisse tout à fait perplexe
l'anneau des séries formelles R[[X]] est bien expliqué dans Cartan
"théorie élémentaire des fonctions analytiques".
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 20 Oct 2008, 10:08
par Maxmau » 20 Oct 2008, 10:08
tize a écrit:Bonjour,
[
Pour Mathelot :
cela me semble possible oui,
=\frac{1}{1-z})
admet un DSE(0) avec un rayon de CV 1 et h(z)=1-cos(z) vaut 0 en 0 et admet un DSE(0)
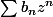
avec un rayon de CV infini, alors si
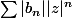
<1 pour
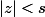
, f

h est DSE(0) avec un rayon de CV au moins égal s
Bonjour
OK pour ton argumentation
Mais comment arriver à la valeur

/2 ?
Mathelot me dit quon utilise des résultats sur les séries formelles (il faudrait que je complète mes connaissances en la matière car à part la définition et quelques résultats
.et je nai pas le « CARTAN » sous la main)
Je signale quune preuve « « élémentaire » du résultat est dans :
Councours ESIM entrepreneur industrie session 2003 filière MP 6 épreuve de mathématiques II (analyse).
Ca se trouve facilement sur le net
Cordialement
Maxmau
PS : Dans le Cartan se trouve aussi une preuve de lanalycité des fonctions holomorphes
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Oct 2008, 12:25
par tize » 20 Oct 2008, 12:25
Dans un message précédent (le #5) il suffit de remarquer (en gardant les même notation) tout
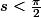
convient, donc le rayon est au moins

mais il ne peut être égal...
Georges Valiron, Cartan, autant de livres que je n'ai jamais lu...pour tout ce qui est complexe j'utilise : Complex Analysis de Serge Lang (il y a plein de belles figures)
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 20 Oct 2008, 12:52
par Maxmau » 20 Oct 2008, 12:52
merci je regarde ça
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
admet un DSE(0) avec un rayon de CV 1 et h(z)=1-cos(z) vaut 0 en 0 et admet un DSE(0)
avec un rayon de CV infini, alors si
<1 pour
, f
h est DSE(0) avec un rayon de CV au moins égal s