Raccordement Sobolev H1

[LaurentOutang]

Bonjour, je cherche à comprendre une équivalence sur les espaces de

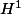
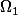
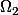
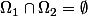
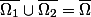
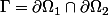
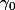
Si l'on considère un domaine borné lipchitzien de et , deux sous-domaines ayant les mêmes propriétés et vérifiant et , alors en notant et l'opérateur de trace Dirichlet, il y a équivalence entre


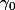
J'arrive à montrer avec la continuité de et la densité de dans mais pour ce qui est de je suis bloqué. Merci de votre aide !

[LaurentOutang]

Sujet résolu en prenant deux suites de fonctions lisses qui tendent vers chacune des solutions des sous-domaines dans le Sobolev correspondant. En utilisant la formule de Green et en passant à la limite, on trouve le gradient faible de la fonction sur tout le domaine.