Raccordement en 1 et -1

par **marawita1** » 17 Fév 2015, 09:51

Bonjour,
C'est ma première question dans ce forum. Je considere l'equation différentielle suivante:
y' - (x / (x^2 -1)) y = 2 x.
1) Résoudre l'équation sur ]- infini, -1[, ]-1,1[ et ]1, + infini[
2)Est ce qu'on peut raccorder les solutions trouvées en -1 et 1 pour obtenir une solution sur tout R.

Pour la première question, c'est bon.
Je suis bloqué au deuxième question.

Merci d'avance.

par **Doraki** » 17 Fév 2015, 10:49

Ben a priori l'équadiff n'a pas de sens en x = +1 ou -1, donc je vois pas trop ce que "être une solution de l'équadiff" peut vouloir dire sur un intervalle qui contient 1 ou -1 (en l'occurence, tout R).

Peut-être qu'ils te demandent les fonctions continues / C1 / Cinfini qui vérifient l'équadiff sur R-{1;-1} ? Dans ce cas-là tu regarde tes solutions et tu vois si il y en a qui peuvent se raccorder à d'autre.

Sinon tu peux réécrire l'équadiff en (x²-1)(y'-2x) - xy = 0. Ce qui a un sens en x=+-1 et donne la condition y=0. De ça on peut en déduire que si t'as des raccordements C1 alors tu auras forcément y(+-1)=0.

par **mathelot** » 17 Fév 2015, 10:51

marawita1 a écrit:Bonjour,
C'est ma première question dans ce forum. Je considere l'equation différentielle suivante:
y' - (x / (x^2 -1)) y = 2 x.
1) Résoudre l'équation sur ]- infini, -1[, ]-1,1[ et ]1, + infini[
2)Est ce qu'on peut raccorder les solutions trouvées en -1 et 1 pour obtenir une solution sur tout R.

Pour la première question, c'est bon.
Je suis bloqué au deuxième question.

Merci d'avance.

bjr,

propriété:
sur un ouvert non connexe,ie, pas un intervalle mais sur la réunion de plusieurs intervalles
une primitive de 1/x est Ln|x|

on résout intervalle par intervalle.

si x>1, la méthode de résolution habituelle par variation de la constante
donne

on fait les calculs sur chaque intervalle. Dans l'intervalle du milieu on a
du ln(1-x^2) à un moment, et une autre constante

sur laquelle pèsent deux conditions de raccordement, une en x=1 et l'autre en x=-1

à compléter...

par **mathelot** » 17 Fév 2015, 10:53

si x>1, la méthode de résolution habituelle par variation de la constante
donne

par **chan79** » 17 Fév 2015, 10:56

marawita1 a écrit:Bonjour,
C'est ma première question dans ce forum. Je considere l'equation différentielle suivante:
y' - (x / (x^2 -1)) y = 2 x.
1) Résoudre l'équation sur ]- infini, -1[, ]-1,1[ et ]1, + infini[
2)Est ce qu'on peut raccorder les solutions trouvées en -1 et 1 pour obtenir une solution sur tout R.

Pour la première question, c'est bon.
Je suis bloqué au deuxième question.

Merci d'avance.

Des valeurs absolues à mettre sous des radicaux peut-être ...

par **marawita1** » 17 Fév 2015, 11:09

donc si j'ai bien compris on ne peut pas parler dans ce cas de raccordement des solutions en -1 et 1
mais si on multiplie l'équation par x^2 -1, ça ne donne pas le résultat!!!!!!!!

par **chan79** » 17 Fév 2015, 11:10

marawita1 a écrit:donc si j'ai bien compris on ne peut pas parler dans ce cas de raccordement des solutions en -1 et 1
mais si on multiplie l'équation par x^2 -1, ça ne donne pas le résultat!!!!!!!!

Tu trouves quoi sur chaque intervalle ?

par **Black Jack** » 17 Fév 2015, 11:12

Je suis comme Doraki,

L'équation donnée, soit y' - (x / (x^2 -1)) y = 2 x n'a pas de sens en x = -1 ou x = +1

Il n'est alors pas question de lui trouver des solutions valables sur R

:zen:

par **marawita1** » 17 Fév 2015, 11:21

ok merci beaucoup pour vos réponses.

par **chan79** » 17 Fév 2015, 12:29

marawita1 a écrit:ok merci beaucoup pour vos réponses.

On doit pouvoir dire que sur chacun des trois intervalles, les solutions sont

OK ?

par **mathelot** » 17 Fév 2015, 12:39

soit

,ie,

où

est une constante de

soit

,ie,

où

est une constante de

au milieu, si

où

est une constante de

on voit qu'un raccord de classe

(fonction continue) est réalisé
par la condition

, et ce, sans condition sur les

comme les dérivées tendent vers l'infini en x=1, le raccord ne peut etre que

par **mathelot** » 17 Fév 2015, 12:41

chan79 a écrit:On doit pouvoir dire que sur chacun des trois intervalles, les solutions sont

OK ?

oui, sans que nécessairement les constantes (par intervalle) soient égales.

par contre, on doit pouvoir trouver des constantes telles que le raccord
géométrique soit de 1ère espèce avec une tangente verticale , point d'inflexion, et
non pas point de rebroussement de 2ème espèce.

Si

, on prend

par **zygomatique** » 17 Fév 2015, 18:15

salut

sur chaque intervalle I_1 = ]-oo, -1[, I_2 = ]-1, 1[ et I_3 = ]1, +oo[ la solution est

où k_i est une constante qui n'est pas la même suivant l'intervalle I_i considéré ...

la seule solution sur R est donc la fonction

en choisissant k_i = 0 pour i = 1, 2, 3

....

par **chan79** » 17 Fév 2015, 20:03

zygomatique a écrit:salut

sur chaque intervalle I_1 = ]-oo, -1[, I_2 = ]-1, 1[ et I_3 = ]1, +oo[ la solution est

....

Avec une valeur absolue sous la racine, non ?

par **zygomatique** » 17 Fév 2015, 20:16

oui bien sur ...

par **chan79** » 17 Fév 2015, 20:28

zygomatique a écrit:salut

sur chaque intervalle I_1 = ]-oo, -1[, I_2 = ]-1, 1[ et I_3 = ]1, +oo[ la solution est

où k_i est une constante qui n'est pas la même suivant l'intervalle I_i considéré ...

la seule solution sur R est donc la fonction en choisissant k_i = 0 pour i = 1, 2, 3

....

Une question
Est-ce qu'on peut dire que y définie par y(x)=2(x²-1), est une solution sur

alors que l'équation différentielle comporte x²-1 au dénominateur ?

par **zaidoun** » 17 Fév 2015, 20:34

Je pense que les réponses de Doraki et black Jack sont les plus proches, en fait on un problème au points 1 et -1.
Par contre si on a l'équation de départ: (x^2 -1)y' - x = 2x (x^2 -1), dans ce cas on peut raccorder les solutions et trouver une solution sur tout R.

par **zygomatique** » 17 Fév 2015, 21:57

l'équation est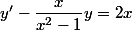

écrite telle quelle l'équation impose donc de l'étudier sur les trois intervalles donnés plus haut

sur chaque intervalle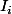

la solution générale est

et plus précisément :

sur l'intervalle ]-oo, -1[ la solution est

sur l'intervalle ]-1, 1[ la solution est

sur l'intervalle ]1, +oo[ la solution est

en choisissant a = b = c = 0 alors

est solution sur chacun des intervalles ....

mais cette fonction a le bon gout d'être définie et continue sur R donc elle se recolle trivialement par prolongement par continuité de R - {-1, 1} à R

(se rappeler qu'une fonction est la donnée d'une formule et d'un ensemble de définition)

elle est donc la seule candidate ...

et évidemment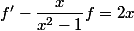

car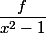

se prolonge à la fonction constante x --> 1

:lol3:

dernière remarque ici ce qui manque à R c'est deux points donc le seul prolongement possible est d'inclure un (ou les deux) point(s) ....

et en multipliant par x²^- 1 alors f vérifie la relation sur R

par **Doraki** » 17 Fév 2015, 22:09

zygomatique a écrit:mais cette fonction a le bon gout d'être définie et continue sur R donc elle se recolle trivialement par prolongement par continuité de R - {-1, 1} à R

(se rappeler qu'une fonction est la donnée d'une formule et d'un ensemble de définition)

elle est donc la seule candidate ...

je ne vois pas pourquoi tu écartes tous les autres recollements continus possibles ?

(et une fonction c'est pas forcément une formule)

par **zaidoun** » 17 Fév 2015, 22:11

@zygomatique: Je pense que le calcul que vous avez fait est valable pour cette équation (surtout au niveau de raccordement): (x^2 -1)y' - x = 2x (x^2 -1).
Pou l'équation de départ c'est autre chose, car tout simplement les deux équations ne sont pas équivalentes.

Raccordement en 1 et -1

Raccordement en 1 et -1

erratum

Qui est en ligne