Question de dm sur les ensembles

[Ainow]

Bonjour,
Je suis bloqué au début d'un DM sur la construction de l'ensemble des réels, voici l'énoncée:
"On considère un ensemble Q (ensemble rationnel) muni de son ordre naturel ⩽, soit A la partie de Q définie par
A = {x ∈ Q +| x²<2}.
et je bloque déjà sur ces deux questions:
1) Montrer que A admet un majorant dans Q.
2)On suppose que α est la borne supérieur de A. soit ε>0 . En remarquant que α -ε n'est pas un majorant, montrer que α² ⩽2.

Pour la 1 je ne sais pas s'il suffit de prendre un nombre rationnel dont la carré est plus grand que 2 ou s'il faut effectuer une démarche particulière.
Pour la deux , comme α est la borne supérieure alors α est le plus petit des majorants donc α - ε étant plus petit que le plus petit des majorants n'est pas un majorant mais je ne vois comment arriver à ce qui est demandé.

[mathelot]

pour la (1)
si donc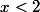
2 est donc un majorant de A

pour la (2) soit
n'est pas un majorant de A
il existe tel que
en élevant au carré

pour tout
donc

[Ainow]

Merci pour votre réponse, en revanche je n'ai pas compris votre dernier raisonnement, lorsque à partir de
(α -ε)²<2 vous avez déduit α²⩽2

[mathelot]

Merci pour votre réponse, en revanche je n'ai pas compris votre dernier raisonnement, lorsque à partir de
(α -ε)²<2 vous avez déduit α²⩽2

on passe à la limite en faisant tendre vers zéro

[Ainow]

Ah d'accord je vois, merci pour votre aide.

[Ainow]

Re-bonjour,
je viens d'apprendre que l'énoncé était incorrect , il faut en fait montrer que α²⩾2, du coup je suis toujours bloqué