Question rapide
21 messages
- Page 1 sur 2 - 1, 2
Question rapide
On écrit d(f(x)) ou alors (d(f))(x) ?
f est une fonction
x un réél
et d une application qui a f associe la différentielle d(f)
f est une fonction
x un réél
et d une application qui a f associe la différentielle d(f)
Disons que E et F sont deux espaces vectoriels normés, que U est un ouvert de E et que f est une application différentiable de U dans F. L'application différentielle de f, c'est une application de quoi dans quoi? Et la différentielle de f en un point x de U, c'est une application de quoi dans quoi? Avec quelle propriété?
Ça devrait répondre à ta question.
Luc
Ça devrait répondre à ta question.
Luc
Aie... :triste:
Commençons par le plus simple : une brave fonction de dans
dans  . On la suppose différentiable en
. On la suppose différentiable en 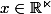
La différentielle de en
en  est une application linéaire de
est une application linéaire de  dans
dans  . On la note
. On la note ) .
.
Maintenant, plus abstrait : l'application différentielle de est une application de
est une application de  dans
dans ) . A tout point
. A tout point  , elle associe une application linéaire,
, elle associe une application linéaire, ) , qui est la différentielle de
, qui est la différentielle de  en
en  .
.
C'est plus clair? :id:
Commençons par le plus simple : une brave fonction de
La différentielle de
Maintenant, plus abstrait : l'application différentielle de
C'est plus clair? :id:
Cryptocatron-11 a écrit:Très clair comme explication. :++:
En fait on a df:=x->df(x) . Ce df(x) est la différentielle de f en x
et une autre application df(x):=h->(df(x))(h)
Tout à fait!
Cryptocatron-11 a écrit: Mais on a aussi une application d:=f->df ?
Très bonne question. Je dirais que si E et F sont des espaces vectoriels normés et U est un ouvert de E, l'application
Cryptocatron-11 a écrit:Et aussi, quelle est la différence entre une forme différentielle et une différentielle ?
Pour ça, je n'ai jamais compris ce qu'est une forme différentielle, je ne vais donc pas pouvoir t'aider pour le moment. Ça viendra peut être prochainement qui sait :we:
Cryptocatron-11 a écrit:J'ai aussi lu que soit f:=U->F et f ' :=U->Lc(E,F)
Lc veut dire application linéaire continu et U est un ouvert de E. ça veut donc dire que (f ' (x)) (x) appartient à F ?
f' est juste une autre notation pour l'application différentielle df, assez pratique. Juste un souci en dimension 1, attention à ne pas confondre f'(x) (une application linéaire) et f'(x) (h) (un vecteur de F).
Du coup j'imagine que c'est plutôt f'(x) (h) et pas f'(x) (x) que tu voulais écrire.
c'est quoi f'(x) pour toi?
et c'est quoi dx?
et c'est quoi le produit f'(x)dx?
Pour une fonction de R dans R, il faut réfléchir au lien entre nombre dérivé, fonction dérivée et différentielle en un point. Le souci étant que si l'on note f'(x) le nombre dérivé en x, la différentielle de f en un point x ce n'est pas f'(x)... C'est la forme linéaire qui multiplie les réels par f'(x). C'est pour ça qu'il vaut mieux faire attention avec la notation f'.
et c'est quoi dx?
et c'est quoi le produit f'(x)dx?
Pour une fonction de R dans R, il faut réfléchir au lien entre nombre dérivé, fonction dérivée et différentielle en un point. Le souci étant que si l'on note f'(x) le nombre dérivé en x, la différentielle de f en un point x ce n'est pas f'(x)... C'est la forme linéaire qui multiplie les réels par f'(x). C'est pour ça qu'il vaut mieux faire attention avec la notation f'.
Luc a écrit:Pour une fonction de R dans R, il faut réfléchir au lien entre nombre dérivé, fonction dérivée et différentielle en un point. Le souci étant que si l'on note f'(x) le nombre dérivé en x, la différentielle de f en un point x ce n'est pas f'(x)... C'est la forme linéaire qui multiplie les réels par f'(x). C'est pour ça qu'il vaut mieux faire attention avec la notation f'.
Dans ce cas là, il faut définir f ' ( x ) comme étant la fonction f ' ( x ) := h -> f ' ( x ) * h , avec h appartenant à E. Et les deux f ' ( x ) (en gras et en rouge) apparaissant dans la définition, veulent dire 2 trucs différents , c'est ça ? Celui que j'ai mis en gras est une forme linéaire et en rouge, c'est le nombre dérivé en x.
c'est quoi f'(x) pour toi?
et c'est quoi dx?
et c'est quoi le produit f'(x)dx?
dx c'est une 1-forme différentielle
f'(x) c'est le nombre dérivé en x
du coup f'(x).dx est aussi une 1-forme différentielle
Cryptocatron-11 a écrit:Dans ce cas là, il faut définir f ' ( x ) comme étant la fonction f ' ( x ) := h -> f ' ( x ) * h , avec h appartenant à E. Et les deux f ' ( x ) (en gras et en rouge) apparaissant dans la définition, veulent dire 2 trucs différents , c'est ça ? Celui que j'ai mis en gras est une forme linéaire et en rouge, c'est le nombre dérivé en x.
Exactement.
Cryptocatron-11 a écrit:dx c'est une 1-forme différentielle
f'(x) c'est le nombre dérivé en x
du coup f'(x).dx est aussi une 1-forme différentielle
Ok. Quelle est l'image d'un vecteur h par dx?
Cryptocatron-11 a écrit:Dans ce cas là, il faut définir f ' ( x ) comme étant la fonction f ' ( x ) := h -> f ' ( x ) * h , avec h appartenant à E. Et les deux f ' ( x ) (en gras et en rouge) apparaissant dans la définition, veulent dire 2 trucs différents , c'est ça ? Celui que j'ai mis en gras est une forme linéaire et en rouge, c'est le nombre dérivé en x.
Et si
En fait ma question revient à demander : est-ce que tu sous-entends 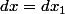 ou pas?
ou pas?
Mais en général, disons que l'on a une base B=(e_1,...,e_n) et x=(x_1,...,x_n) dans cette base. Est-ce qu'on a le droit de définir une 1-forme en disant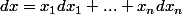 ? En notant
? En notant 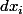 la forme linéaire coordonnée qui à un vecteur
la forme linéaire coordonnée qui à un vecteur  associe
associe 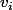 , sa i-ème coordonnée dans la base B. (je précise que je connais pas la réponse, c'est une vraie question).
, sa i-ème coordonnée dans la base B. (je précise que je connais pas la réponse, c'est une vraie question).
Mais en général, disons que l'on a une base B=(e_1,...,e_n) et x=(x_1,...,x_n) dans cette base. Est-ce qu'on a le droit de définir une 1-forme en disant
Luc a écrit:En fait ma question revient à demander : est-ce que tu sous-entendsou pas?
Vu que
Luc a écrit:Mais en général, disons que l'on a une base B=(e_1,...,e_n) et x=(x_1,...,x_n) dans cette base. Est-ce qu'on a le droit de définir une 1-forme en disant? En notant
la forme linéaire coordonnée qui à un vecteur
associe
, sa i-ème coordonnée dans la base B. (je précise que je connais pas la réponse, c'est une vraie question).
ben vu que
Mais dans mon exemple, je crois que tout les
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
