Quelques question sujet BCPST agro veto 2014
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 22 Nov 2014, 19:43
par kaltasus » 22 Nov 2014, 19:43
Bonsoir à tous,
J'aurais quelques questions à vous poser sur un sujet d'algèbre (MATHS A AGRO 2014)
Le sujet est disponible ici :
https://www.concours-agro-veto.net/IMG/pdf_BCPST_sujet_de_mathematiques_epreuve_A_2014.pdfet il me faudrait de l'aide pour la question 3)1)2): je suis tenté de dire que Q étant matrice de passage, Q inversible, donc rg(Q) = 3
or si a=b=c=0, on a rg(Q) =<3 donc nécessairement, il faut au moins un terme sur les 3 qui soit non nul ?
Je veux bien de l'aide pour la 3)1)4 aussi si vous avez une idée !! merci bien en tout cas

Cordialement
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 22 Nov 2014, 23:06
par mrif » 22 Nov 2014, 23:06
Pour la 3.1.2 je te suggère d'utiliser ces 2 résultats:
- Une matrice de passage est inversible.
- Une matrice est inversible SSI son déterminant est non nul
Pour la 3.1.4, une condition nécessaire est suffisante pour qu'un vecteur appartienne à F est que sa troisième coordonnée dans la nouvelle base U est nulle. Or, dans la question précédente, tu as montré que cette troisième coordonnée est donnée par:
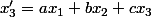
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 22 Nov 2014, 23:19
par kaltasus » 22 Nov 2014, 23:19
C'est bon j'y suis parvenu !!!
pour la 3.2.1, une fois que j'ai montré que la matrice a bien cette forme, et l'égalité avec les transposées, comment en déduire que (a;b;c) valeur propre de transp(A) ?
merci pour ton aide
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 22 Nov 2014, 23:51
par mrif » 22 Nov 2014, 23:51
kaltasus a écrit:C'est bon j'y suis parvenu !!!
pour la 3.2.1, une fois que j'ai montré que la matrice a bien cette forme, et l'égalité avec les transposées, comment en déduire que (a;b;c) valeur propre de transp(A) ?
merci pour ton aide
Tu appliques l'égalité
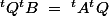
au vecteur (0,0,1)
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 22 Nov 2014, 23:53
par kaltasus » 22 Nov 2014, 23:53
C'est à dire (appliquer une égalité à un vecteur ??)?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 00:01
par mrif » 23 Nov 2014, 00:01
Chaque membre de l'égalité est une matrice (le produit de 2 matrices est une matrice). Tu calcules l'image du vecteur (0,0,1) par ces 2 membres et tu trouveras:
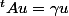
où
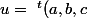)
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 00:16
par kaltasus » 23 Nov 2014, 00:16
Ca fonctionne et je trouve bien ça, mais pourquoi on multiplies par (0,0,1) ? comment on le devine ??
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 00:43
par mrif » 23 Nov 2014, 00:43
kaltasus a écrit:Ca fonctionne et je trouve bien ça, mais pourquoi on multiplies par (0,0,1) ? comment on le devine ??
Tu cherches à calculer
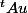
et tu disposes de l'égalité:
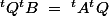
alors une idée mécanique est de se dire est ce que je peux trouver un vecteur v tel que
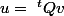
?
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 00:47
par kaltasus » 23 Nov 2014, 00:47
Ça marche je vois l'idée, merci beaucoup,
une dernière petite question (tu peux juste me donner une indication si tu veux, je suis prêt à chercher c'est un dm donc je le fais surtout pour réfléchir !!)
à la 3.2.2, j'ai montré a y1 + b y2 + c y3 = lambda (a x1 + b x2 + c x3)
Ensuite comment déduire F stable par f de cette égalité ? merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Nov 2014, 00:56
par Ben314 » 23 Nov 2014, 00:56
Salut,
Utilise la caractérisation de F vue au 3.1.4
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 00:58
par mrif » 23 Nov 2014, 00:58
kaltasus a écrit:Ça marche je vois l'idée, merci beaucoup,
une dernière petite question (tu peux juste me donner une indication si tu veux, je suis prêt à chercher c'est un dm donc je le fais surtout pour réfléchir !!)
à la 3.2.2, j'ai montré a y1 + b y2 + c y3 = lambda (a x1 + b x2 + c x3)
Ensuite comment déduire F stable par f de cette égalité ? merci
Tu as montré dans une question précédente q'une CNS pour qu'un vecteur
)
appartienne à F est
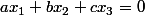
.
Le reste saute aux yeux et si tu ne vois pas je détaillerai.
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 01:04
par kaltasus » 23 Nov 2014, 01:04
On écrit donc a x1 + b x2 + c x3 = 0 donc a y1 + b y2 + c y3 =0 ?
et ensuite ?
de plus, on a pas de condition sur la stabilité ? c'est toujours vrai ?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 01:14
par mrif » 23 Nov 2014, 01:14
kaltasus a écrit:On écrit donc a x1 + b x2 + c x3 = 0 donc a y1 + b y2 + c y3 =0 ?
et ensuite ?
de plus, on a pas de condition sur la stabilité ? c'est toujours vrai ?
Soit
)
un élément de F on a
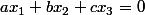
Comme
 = (y_1,y_2,y_3) \ et \ que \ ay_1+by_2+cy_3 = 0)
, on en déduit que
)
appartient à F donc
)
appartient à F donc F est stable par f
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 01:18
par kaltasus » 23 Nov 2014, 01:18
ah d'accord le résultat est aussi vrai pour f(x1,x2,x3) !!!
Ca me semble évident une fois que vous l'écrivez :)
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 01:24
par kaltasus » 23 Nov 2014, 01:24
Pour déterminer les espaces stables par f à la 4), il faut déterminer le polynome caractéristique, et déterminer les valeurs propres et sous espaces propres ?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 01:27
par mrif » 23 Nov 2014, 01:27
kaltasus a écrit:ah d'accord le résultat est aussi vrai pour f(x1,x2,x3) !!!
Ca me semble évident une fois que vous l'écrivez

Il y avait une erreur d'inattention que je viens de corriger dans mon dernier message.
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 23 Nov 2014, 01:31
par mrif » 23 Nov 2014, 01:31
kaltasus a écrit:Pour déterminer les espaces stables par f à la 4), il faut déterminer le polynome caractéristique, et déterminer les valeurs propres et sous espaces propres ?
Oui
Bon courage
-
kaltasus
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Nov 2014, 19:38
-
 par kaltasus » 23 Nov 2014, 01:44
par kaltasus » 23 Nov 2014, 01:44
Je trouve 2 valeur propre triple, et le sous espace propre associé est vect(1,1,-1) ?
est-ce que c'est ce qui est demandé ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
