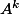Bonjour, issoram, voici l'énoncé avec ce que j'ai trouvé :
Dans l'espace euclidien (avec le produit scalaire canonique de R^3 et la norme euclidienne associée)
Soit u un endormorphisme de E=R^3 de matrice dans la base canonique

,
A =
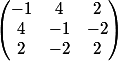
1)
trouver le polynome caractéristique de u,
 = det(u - \lambda * id_E))
fait :
 = 42 - 5\lambda - \lambda^3)
2)
vérifier que
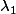
= 3 est une valeur propre de u
trouver un base du sous espace propre

associé à
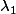
Vérifier que
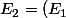^\perp)
est un sous espace propre
fait :
Le polynôme n'admet pas d'autre solution dans

la base de

est
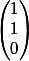
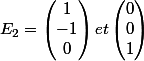
choisi pour que ce soit orthogonal à

par contre, je ne vois pas comment vérifier que

est un sous-espace propre
3)Trouver la matrice
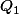
dans la base canonique de

de la projection orthogonale
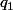
sur

, puis la matrice
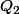
dans la base canonique de

de la projection orthogonale
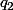
sur

fait
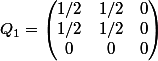
et
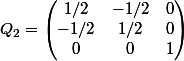
4) Soit un entier

. Déterminer
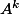
en fonction de
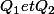
Je ne vois pas comment faire.
Je ne vois pas quelles propriétés de
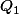
et
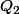
me permettent de calculer