Prouver une suite de Cauchy Cn = An * Bn (An et Bn Cauchy)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
oxsase97
- Membre Naturel
- Messages: 16
- Enregistré le: 02 Nov 2018, 15:16
-
 par oxsase97 » 02 Nov 2018, 15:21
par oxsase97 » 02 Nov 2018, 15:21
Bonjour à tous,
Je me permets de vous déranger durant cette après-midi pluvieuse (chez moi en tout cas) pour vous poser une petite question:
Je dois démontrer, dans un devoir, que la suite Cn = An * Bn est une suite de Cauchy, sachant que An et Bn sont elles des suites de Cauchy.
Merci d'avance à tous et bon weekend

-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 02 Nov 2018, 15:32
par jlb » 02 Nov 2018, 15:32
Ecris C_(n+p) - C_n = A_(n+p)B_(n+p) - A_(n+p)Bn + A_(n+p) Bn - A_nB_n et essaie de modifier cela pour utiliser que AN et Bn sont de Cauchy ( il faudra aussi utliser le fait qu'une suite de Cauchy est bornée)
-
mathelot
 par mathelot » 02 Nov 2018, 15:35
par mathelot » 02 Nov 2018, 15:35
bonjour,
il faut prouver d'abord qu'une suite de Cauchy est bornée.
écrire ensuite pour m et n entiers
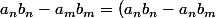+(a_nb_m-a_mb_m))
et appliquer l'inégalité triangulaire
désolé jlb je n'avais pas vu ton message..
-
oxsase97
- Membre Naturel
- Messages: 16
- Enregistré le: 02 Nov 2018, 15:16
-
 par oxsase97 » 03 Nov 2018, 10:05
par oxsase97 » 03 Nov 2018, 10:05
Merci beaucoup j'ai réussi

Bon samedi à vous deux.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
