Prouver l'existence d'une application

[zaidoun]

Tu parles sur l'existence et l'unicité d'une telle application linéaire?

Si oui, une application linéaire est entièrement caractérisée par la donnée des images des vecteurs d'une base.

[zaidoun]

oui, mais si je vous donne des vecteurs et leurs images par f, alors si on vérifie que ces vecteurs forment une base, alors nécessairement cette application f existe et elle est unique aussi, et c'est facile de déterminer l'expression explicite de f.

[zaidoun]

c'est un résultat du cours par exemple voir ce lien: http://gilles.costantini.pagesperso-orange.fr/agreg_fichiers/dimevrg.pdf (page 7).

[Ben314]

@zaidoun : je ne pense pas que tu réponde à la question posé par Redécouverte.

@Redécouverte : Pour montrer qu'une fonction f vérifiant blablabla existe est est unique, on procède effectivement assez systématiquement de façon "vicieuse", en commençant par :
1) Si une telle application f existe alors elle doit vérifier ..... donc on a forcément f=... et cela prouve que, si une telle f existe, ça ne peut être que celle là (i.e. que, si elle existe, elle est unique).
2) Comme dans les calculs du 1), on a presque toujours raisonné par implication, c'est à dire que l'on a uniquement montré que (f vérifie blablabla) => (f=...) il faut maintenant montrer la réciproque, c'est à dire que (f=...) => (f vérifie blablabla) pour s'assurer que la fonction f trouvée au 1) est effectivement une solution du problème (et donc que le problème a une unique solution).
Il peut arriver que pour la réciproque, ça déconne, c'est à dire que la fonction f trouvée au 1) ne vérifie pas blablabla et cela prouve qu'il n'existe aucune fonction vérifiant blablabla vu que la fonction f en question était l'unique candidat possible.

Résumé rapide : tu cherche à montrer que (f vérifie blablabla) <=> (f=...) et tu fait une "double implication" ce qui est très naturel. Ce qui l'est peut-être un peu moins au début, c'est de commencer par =>, mais on n'a pas bien le choix vu qu'en général on ne connait pas f au début.

[Ben314]

Pour te donner un exemple un peu plus simple où ce que l'on cherche est un réel (ou un complexe) plutôt qu'une fonction, il y a le "grand classique" suivant (souvent présenté comme un pseudo "paradoxe" ) :

On veut résoudre (dans R ou dans C) l'équation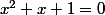 (E)

(1) Supposons qu'un réel (ou complexe) x vérifie .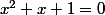
Alors, en multipliant par x, on en déduit que donc que , c'est à dire que
là, il apparait assez clairement que, vu le bricolage infâme qu'on a fait, on n'a pas du tout procédé par équivalence mais par simple implication

(1.a) Dans R, l'unique solution de l'équation est .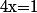
Et c'est là que c'est présente comme un pseudo "paradoxe" vu que 1 n'est pas du tout solution de x²+x+1=0, mais si on comprend bien ce qu'on a écrit, il faut continuer le raisonnement en écrivant que :
Cela montre que, si x²+x+1=0 admet une solution dans R, cette solution ne peut être que x=1.
(2.a) Sauf que 1²+1+1 est non nul et cela prouve que l'équation en question n'a pas de solution dans R.

(1.b) Dans C, les trois solutions de l'équation sont , , .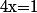
Cela montre que, si x²+x+1=0 admet des solutions dans C, ces solutions font partie des 3 çi dessus.
(2.b) Sauf que 1²+1+1 est non nul donc 1 n'est pas une solution de (E) et par contre, on vérifie que les deux autres marchent.

J'espère que tu comprend que, lorsque c'est par exemple une fonction que l'on cherche, le principe est le même : en deux temps (1) : "si f est solution alors f=..." et (2) "si f=... alors f est (ou pas) solution"

[Ben314]

Merci pour cet exemple très clair : en fait, on "restreint" dans un premier temps les possibilités de solutions, puis on vérifie que cette ou ces solutions fonctionnent. si c'est le cas parmi cette ou ces solutions possibles, la ou les solutions existent effectivement, sinon non.

C'est exactement ça, sachant qu'en algèbre linéaire, quasi systématiquement on ne trouve qu'un seul "candidat" susceptible de marcher et que quasi systématiquement, il s'avère que le "candidat" en question marche effectivement.

C'est en particulier pour ça que je t'ai donné un exemple avec une équation où on trouve (dans le cas complexe) trois "candidats" dont seuls deux sont effectivement des solutions : il me semble qu'on comprend mieux le principe dans ce cas.

[zygomatique]

Merci pour cet exemple très clair : en fait, on "restreint" dans un premier temps les possibilités de solutions, puis on vérifie que cette ou ces solutions fonctionnent. si c'est le cas parmi cette ou ces solutions possibles, la ou les solutions existent effectivement, sinon non.

salut

je ne suis pas d'accord ...

pour reprendre l'exemple de Ben314

pour que il est nécessaire que

si S est l'ensemble des solutions de (1) et T celui de (2) alors on a donc ::



"on ne restreint pas" pas puisqu'on en prend plus que de possibles !!!

certes passer de R (ou C) à T est tout de même une sacré "restriction" :ptdr:

et tout le problème ensuite est la réciproque : passer de (2) à (1) : de T à S (en supprimant certaines éventualités)

:lol3:

et pour préciser ce que fait Ben314 : il rajoute une solution en multipliant par (x - 1) ...

ou alors il multiplie par 0 .... :lol3:

[zygomatique]

n'est-ce pas ce que je dis ensuite ?

[zygomatique]

ben si on a :

f vérifie P <==> f vérifie A et B

et

f vérifie P ==> f = s

et

s vérifie A et B

alors

s vérifie P

et

f = s