Bonsoir, je m'adresse à vous dans l'espoir d'obtenir de l'aide sur un exo coriace :
On dispose de deux ensembles

tous deux non vides sur lesquels on définit respectivement une relation d'équivalence

, et soit

une application.
On suppose également que, quel+s que soient
 R' f(y))
.
Je dois donc montrer qu'il existe une
unique application

de

dans

qui, à toute classe d'équivalence de

, associe la classe d'équivalence de
)
, mais je ne vois vraiment pas du tout comment faire...
J'ai pensé à utiliser le théorème fondamental suivant :
Pour

une relation d'équivalence sur un ensemble non vide

, et
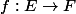
une application constante sur les classes d'équivalences, alors il existe une unique application

telle que

où

désigne la projection canonique de

sur

.
J'ai essayé aussi d'exploiter la notion de diagramme qui commute (donné avec ce théorème pour visualiser quelque chose, mais rien).
Merci d'avance pour votre aide :++:
