On suppose qu'une fonction
En théorie il faudrait établir le développement en série entière de
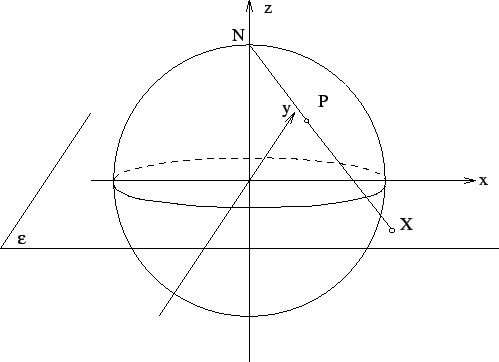
AlexisD a écrit:Voici comment j'ai procédé: d'abord une fonction à valeurs dans S² est holomorphe ensi:
-ou bienet
est holomorphe en
-ou bienet
est holomorphe en
Doraki a écrit:Tes fonctions, c'est Pn (x,y,z) = (x + iy)(1+z)/(1-z) et Ps (x,y,z) = (x + iy)(1-z)/(1+z) ?
Doraki a écrit:On est pas censé avoir que si f(z0) est différent de N et de S, ces deux machins sont équivalents ?
un peu bizaroïde du fait que, sauf erreur, siAlexisD a écrit:une fonction à valeurs dans S² est holomorphe ensi:
-ou bienet
est holomorphe en
-ou bienet
est holomorphe en
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :