Projection orthogonale: petit rappel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 20:20
par Kimou » 21 Fév 2010, 20:20
Bonjour,
j'ai quelques questions concernant la projection orthogonale je vous met mes énoncés:
ENONCE 1:"Determiner la matrice dans la base canonique de
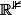
de la projection orthogonale sur le plan d'équation
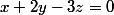
"
ENONCE 2:
"Determiner la matrice dans la base canonique de
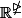
de la projection orthogonale sur l'espace vectoriel
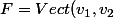)
engendré par les vecteur
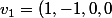)
et
)
"
QUESTIONS:1)exercice 1:Pourquoi est ce logique vis a vis de l'enoncé que le rang soit 2 alors qu'on projète une droite?
2)exercice 1: Mon prof nous a corrigé cet exo mais il est passée par 2 matrices (la deuxième étant la bonne avec(
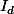
- (la premiere matrice))
3)Exercice 2: en refaisant exactement pareil je trouve une matrice et d'après le corrigé c'est directement celle ci qui répond à la question. Or moi j'aurais envi de faire comme l'exo 1 à savoir ((Matice identité) - (celle que j'ai trouvée) pourquoi est-ce faux? est-ce lui qui n'a pas fini?
Merci beaucoup!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Fév 2010, 21:01
par Nightmare » 21 Fév 2010, 21:01
Salut,
"on projète une droite" ? Je n'ai pas vraiment compris. Il n'est nullement question de droite dans l'énoncé 1 ...
Pour la suite des questions, il aurait peut être été judicieux que tu nous donnes les matrices en question ...
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 21:42
par Kimou » 21 Fév 2010, 21:42
Nightmare a écrit:Salut,
"on projète une droite" ? Je n'ai pas vraiment compris. Il n'est nullement question de droite dans l'énoncé 1 ...
Pour la suite des questions, il aurait peut être été judicieux que tu nous donnes les matrices en question ...
les matrices de l'exo 1 sont:
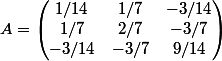
puis le prof a fait:
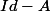
ce qui nous donne au final:
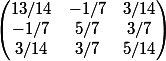
L'exercice 2 la matrice finale est seulement:

Et ne fait pas
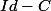
En ce qui concerne la droite on est dans un espace de dimension 3 et on projète sur un plan de dimension 2 donc j'en est déduis que l'orthogonal était forcément engendré par un seul vecteur donc une droite non?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 22:17
par Ben314 » 21 Fév 2010, 22:17
Salut,
Dans l'exercice 1, ton prof a considéré que, pour trouver la matrice de la projection orthogonale sur LE PLAN x+2y-3z=0, il était plus rapide de commencer par chercher la matrice de la projection orthogonale sur LA DROITE orthogonale au plan : cette matrice est A (de rang 1 : tout les vecteurs colonnes sont des vecteurs normaux du plan).
Ensuite, effectivement, pour trouver la matrice de la projection orthogonale sur le plan, il n'y a plus qu'a considérer B=Id-A (la somme des deux projections est bien sûr l'identité) qui elle est évidement de rang 2.
Pour l'exo 2) , on demande de déterminer la matrice d'une projection de E=R^4 sur un s.e.v. F de dim 2. Comme l'orthogonal de F est de dim 4-2=2, "l'astuce" du premier exercice n'a absolument aucun intérêt ici donc il calcule directement la matrice de la proj. orthogonale sur F.
Bien sûr, en considérant D=Id-C, on obtient la matrice de la projection orthogonale de E sur l'orthogonal de F, mais comme ce n'est pas demandé et que de calculer C ou D est de "même difficulté"...
(Tu peut évidement vérifier que C et D sont de rang 2)
P.S. : il y a une erreur dans ta matrice C : le dernier vecteur colonne n'est pas dans F...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 22:23
par Kimou » 21 Fév 2010, 22:23
Ben314 a écrit:Salut,
Dans l'exercice 1, ton prof a considéré que, pour trouver la matrice de la projection orthogonale sur LE PLAN x+2y-3z=0, il était plus rapide de commencer par chercher la matrice de la projection orthogonale sur LA DROITE orthogonale au plan : cette matrice est A (de rang 1 : tout les vecteurs colonnes sont des vecteurs normaux du plan).
Ensuite, effectivement, pour trouver la matrice de la projection orthogonale sur le plan, il n'y a plus qu'a considérer B=Id-A (la somme des deux projections est bien sûr l'identité) qui elle est évidement de rang 2.
Pour l'exo 2) , on demande de déterminer la matrice d'une projection de E=R^4 sur un s.e.v. F de dim 2. Comme l'orthogonal de F est de dim 4-2=2, "l'astuce" du premier exercice n'a absolument aucun intérêt ici donc il calcule directement la matrice de la proj. orthogonale sur F.
Bien sûr, en considérant D=Id-C, on obtient la matrice de la projection orthogonale de E sur l'orthogonal de F, mais comme ce n'est pas demandé et que de calculer C ou D est de "même difficulté"...
(Tu peut évidement vérifier que C et D sont de rang 2)
Merci tu m'a un peu eclairer le seul probleme que je me pose c'est moi en faisant exactement les meme type de calcul dans l'exo 1 puis dans l'exo 2 je trouve A dans 1 et je trouve la bonne matrice dans 2... Comment savoir si je dois faire l'astuce de l'identité ou laisser la matrice finale tel quel?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 22:32
par Ben314 » 21 Fév 2010, 22:32
Ben...
Lorsque tu fait tes calcul, normalement, tu devrais savoir dés le début qu'est-ce que tu calcule !!!!!
Si tu calcule ce que l'on t'a demandé (i.e. la projection orthogonale sur F) alors tu donne le résultat tel quel (ce qui me parrait normal, vu que tu as calculé... ce que l'on t'as demandé)
Si tu commence par calculer la projection sur l'orthogonal de F (qui n'est pas celle demandée) alors à la fin tu prend Id-la_matrice_trouvée...
Aprés, si la question est "quand doit on utiliser l'astuce", c'est toi qui voit...(a mon avis c'est interessant surtout pour les projection sur des "hyperplans", c'est à dire sur des s.e.v. de dimension un de moins que la dimension totale de l'espace)
Essaye par exemple de faire l'exercice 1 sans utiliser d'astuce : tu constatera (peut-être) que c'est un peu plus long...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 22:32
par Kimou » 21 Fév 2010, 22:32
c'est bon j'ai rectifié la matrice...
En fait je comprend parfaitement ce que tu ma expliqué seulement dans le deuxieme cas tu me dis que ce n'est aps demandé or c'est la même question dans les deux exos non? ou c'est moi qui en comprend pas trop visuellement dans ce cas la difference entre les enoncés (sans prendre en compte qu'il s'agit de deux espaces de diemension différente bien entendu)... dans le sdeux cas on nous demande bien de déterminer la matrice de la projkection orthogonalesur le plan (1) ou F (en 2) non?
merci
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 22:34
par Kimou » 21 Fév 2010, 22:34
Essaye par exemple de faire l'exercice 1 sans utiliser d'astuce : tu constatera (peut-être) que c'est un peu plus long...
Non justement ce que je te dis c'est qu' en le refaisant de la meme façon que l'exo 2 je tombe sur A!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 22:41
par Ben314 » 21 Fév 2010, 22:41
Oui, effectivement, c'est deux fois la même question, mais avec des "valeurs numériques" différentes.
Trés souvent (pour ne pas dire tout le temps), il y a plusieurs méthodes pour répondre à une même question, et, en fonction du contexte, certaines de ces méthodes sont plus rapides que d'autres :
Ici, dans le premier exo, la "méthode" consistant à commencer à calculer la projection sur l'orthogonal de F est (sans doute) plus rapide que de chercher directement la projection sur F, par contre dans le deuxiéme exo, il est plus rapide de chercher directement la projection sur F.
J'insiste : essaye de faire l'exo 1 avec la méthode que le prof a employé pour l'exo 2 : tu trouvera bien sûr le bon résultat, mais les calculs seront plus long.
De même, tu peut essayer dans l'exo 2 de chercher d'abord la projection sur l'orthogonal de F et tu verra que... ça ralonge les calculs...
En algèbre linéaire (c'est la "théorie" des E.V.) il y a toujours tout plein de méthodes pour faire un exo. La grosse astuce, c'est d'arriver à choisir la plus rapide...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 22:43
par Ben314 » 21 Fév 2010, 22:43
Kimou a écrit:Non justement ce que je te dis c'est qu' en le refaisant de la meme façon que l'exo 2 je tombe sur A!
Explique un peu comment tu as procédé, on te dira où ca "coince"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 22:50
par Kimou » 21 Fév 2010, 22:50
Dans le premier exo je fais ainsi:
avec e1 e2...vecteurs dans la base canonique
P(e1)=(e1|n)n
P(e2)=(e2|n)n
P(e3)=(e3|n)n
où (.|.)est le produit scalaire
n le vecteur orthogonal au plan qu'on trouve facilement grâce à l'equation (ce sont les coeffs) et que je normalise par la suite...
et je trouve la matrice A
Exo 2 je fais pareil sauf qu'au debut j'ai pas de vecteur orthonormal
je fais donc Gram shmidt j'ai deux vecteurs: u1 et u2 qui engendrent l'orthogonal de F.
je fais pareil P(e1)=(e1|u1)u1 + (e1|u2)u2
etc...
et là je trouve la bonne matrice directement. Quel est mon erreur? c'est cela que je ne comprend pas la différence de raisonement que je fais entre les deux exos?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 23:01
par Ben314 » 21 Fév 2010, 23:01
Dans l'exo 1, ton le fameux vecteur normal unitaire 'n' constitue a lui tout seul une base de l'orthogonal de F donc la projection que tu calcule est celle sur l'orthogonal de F.
Dans l'exo2, je soupçonnerais bien que tu as appliqué Gram-Schmidt aux deux vecteurs V1 et V2 de l'énoncé donc ta base orthonormée {U1,U2} est une base de F et la projection que tu calcule est celle sur F.
Dans l'exo 1, si tu veut directement la projection sur F, il te faut une base de F. Pour cela, tire au pif deux vecteurs (linéairement indépendants) W1 et W2 vérifiant x+2y-3z=0, puis applique la même méthode qu'a l'exo 2 : tu trouvera le bon résultat directement... mais c'est plus long !!
Si tu voulais dans l'exo 2 commencer par trouver la projection sur l'orthogonal de F, il faudrait commencer par trouver une base de cet orthogonal. Saurait tu trouver (assez rapidement) une telle base ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 23:07
par Kimou » 21 Fév 2010, 23:07
Ben314 a écrit:Dans l'exo 1, ton le fameux vecteur normal unitaire 'n' constitue a lui tout seul une base de l'orthogonal de F donc la projection que tu calcule est celle sur l'orthogonal de F.
Dans l'exo2, je soupçonnerais bien que tu as appliqué Gramm-Schmidt aux deux vecteurs V1 et V2 de l'énoncé donc ta base orthonormée {U1,U2} est une base de F et la projection que tu calcule est celle sur F.
Dans l'exo 1, si tu veut directement la projection sur F, il te faut une base de F. Pour cela, tire au pif deux vecteurs (linéairement indépendants) W1 et W2 vérifiant x+2y-3z=0, puis applique la même méthode qu'a l'exo 2 : tu trouvera le bon résultat directement... mais c'est plus long !!
Si tu voulais dans l'exo 2 commencer par trouver la projection sur l'orthogonal de F, il faudrait commencer par trouver une base de cet orthogonal. Saurait tu trouver (assez rapidement) une telle base ?
Je suis perdu.. si j'applique ce que j'ai fait avant avec u1 et u2 c'est justement pour avoir des vecteurs orthogonaux(grace à Gram Schmidt) à F je ne comprend pas pourquoi il s'agit de vecteur appartenant à F et non a F orthogonal?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 23:17
par Ben314 » 21 Fév 2010, 23:17
Bon, tout dépend de ce que tu appelle "appliquer gram-schmidt" :
1) Pour moi, dans le contexte présent, cela veut dire partir de V1 et V2, "redresser" V2 pour le rendre perpendiculaire à V1 puis diviser les deux vecteurs obtenus par leur normes pour obtenir U1 et U2.
En faisant cela, tu obtient rapidement une base orthonormée de F.
2) L'autre possibilité est de partir d'une base {V1,V2,V3,V4} de R^4 (tu choisi plus ou moins au pif deux vecteurs V3 et V4 pour compléter en une base de R^4) puis tu applique gram-schmidt à ces 4 vecteurs : c'est beaucoup plus long. Tu obtient aprés calcul une base orthonormée {U1,U2,U3,U4} de R^4 qui est telle que {U1,U2} est une base orthonormée de F et {U3,U4} une base orthonormée de l'orthogonal de F.
Cette deuxième possibilité est, à mon avis, beaucoup beaucoup trop longue vu le but de l'exercice (mais elle marche !!!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 23:23
par Kimou » 21 Fév 2010, 23:23
Ben314 a écrit:Bon, tout dépend de ce que tu appelle "appliquer gram-schmidt" :
1) Pour moi, dans le contexte présent, cela veut dire partir de V1 et V2, "redresser" V2 pour le rendre perpendiculaire à V1 puis diviser les deux vecteurs obtenus par leur normes pour obtenir U1 et U2.
En faisant cela, tu obtient rapidement une base orthonormée de F.
2) L'autre possibilité est de partir d'une base {V1,V2,V3,V4} de R^4 (tu choisi plus ou moins au pif deux vecteurs V3 et V4 pour compléter en une base de R^4) puis tu applique gram-schmidt à ces 4 vecteurs : c'est beaucoup plus long. Tu obtient aprés calcul une base orthonormée {U1,U2,U3,U4} de R^4 qui est telle que {U1,U2} est une base orthonormée de F et {U3,U4} une base orthonormée de l'orthogonal de F.
Cette deuxième possibilité est, à mon avis, beaucoup beaucoup trop longue vu le but de l'exercice (mais elle marche !!!)
Oui en effet je fais la solution numéro une... Je cherche deux vecteurs appartenant à l'orthogonal de F afin qu'on est une somme directe entre F et F-orthogonal =
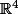
et avec u1 = v1.
Donc dans le premier exo je cherche n appartenant a F-orthogonal et dans l'autre exo je cherche u1 et u2 appartenant à F orthogonal... jusque là c'est la même chose non?
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 23:33
par Kimou » 21 Fév 2010, 23:33
En appliquant Gram schmidt cela revient bien à creer une base orthogonal normée à l'espace que l'on considère (pour nous F engendrée par v1 et v2)?
Je pense avoir un problème de définition quelque part mais je ne sais pas trop où! :hein:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 21 Fév 2010, 23:35
par Ben314 » 21 Fév 2010, 23:35
Si c'est le 1) que tu fait, alors les vecteurs U1 et U2 que tu obtient sont toujours dans F (car V1 et V2 étaient dans F).
Le procédé de Gram-Schmidt appliqué à une base d'un sous espace vectoriel F donne une base orthonormée du même sous espace vectoriel F.
Essaye de visualiser à quoi correspondent les calculs de Gram-Schmidt dans le cas d'une base (formée de deux vecteurs) d'un plan dans l'espace de dim 3 : tu ajoute/retranche au deuxième vecteur un certain nombre de fois le premier pour le rendre perpendiculaire au premier puis tu divise les deux vecteurs par leur norme.
Tout cela reste dans le même plan (en fait c'est le but du jeu !!!) la seule chose qui as changé c'est qu'au début tu avait une base "toute dégueu" du plan et qu'a la fin tu as une base orthonormée... du même plan !
Dans l'exo 1 tu as aussi appliqué Gram-Schmidt (en divisant le vecteur normal du plan pa sa norme) mais l'énorme différence, c'est que dans cet exo 1, tu est parti d'un vecteur orthogonal à F et pas de vecteurs de F comme dans le 2.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kimou
- Membre Relatif
- Messages: 250
- Enregistré le: 30 Oct 2005, 10:46
-
 par Kimou » 21 Fév 2010, 23:38
par Kimou » 21 Fév 2010, 23:38
Ben314 a écrit:Si c'est le 1) que tu fait, alors les vecteurs U1 et U2 que tu obtient sont toujours dans F (car V1 et V2 étaient dans F).
Le procédé de Gram-Schmidt appliqué à une base d'un sous espace vectoriel F donne une base orthonormée du même sous espace vectoriel F.
Essaye de visualiser à quoi correspondent les calculs de Gram-Schmidt dans le cas d'une base (formée de deux vecteurs) d'un plan dans l'espace de dim 3 : tu ajoute/retranche au deuxième vecteur un certain nombre de fois le premier pour le rendre perpendiculaire au premier puis tu divise les deux vecteurs par leur norme.
Tout cela reste dans le même plan (en fait c'est le but du jeu !!!) la seule chose qui as changé c'est qu'au début tu avait une base "toute dégueu" du plan et qu'a la fin tu as une base orthonormée... du même plan !
Dans l'exo 1 tu as aussi appliqué Gram-Schmidt (en divisant le vecteur normal du plan pa sa norme) mais l'énorme différence, c'est que dans cet exo 1, tu est parti d'un vecteur orthogonal à F et pas de vecteurs de F comme dans le 2.
Je te remercie beaucoup pour l'aide que tu m'a apporté ce soir, je vais méditer dessus et te souhaite une bonne nuit (car je ne suis pas en vacances^^).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
