Projecteurs

[Ilham]

Bonjour tout le monde
Je veux savoir s'il vous plaît comment je expliciter un projecteur sur F et suivant G
Avec F=vect(2,1,1)
Et G=(x ,y,z / x=z)
Pouvez-vous me donner une indication ?
Merci d'avance^-^

[Mateo_13]

Bonjour,

Et G est le plan d'équation

Il y a peut-être une solution plus simple que je ne connais pas, mais j'essaie :
Trouve une base de l'espace à trois dimensions dont le premier vecteur est ,
et les deux autres vecteurs (que tu dois exprimer en fonction de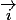 , 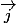et 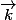) sont dans le pan d'équation (un dessin peut t'aider à les trouver).

Ensuite tout vecteur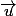 de l'espace a des coordonnées dans cette base, et la projection sur suivant G sera l'application qui à associe un vecteur de quelles coordonnées à ton avis ?

Cordialement,
--
Mateo.

[Ilham]

Merci bcp pour votre réponse
Mais dans le cours on n'a pas la notion de dimension , c'est pour les MP
^-^ merci

[Mateo_13]

Mais dans le cours on n'a pas la notion de dimension , c'est pour les MP

Moi non plus je n'ai pas besoin de la notion de dimension,
c'est une autre manière de dire que les vecteurs ont trois coordonnées.

Arrives-tu à trouver une base simple du plan G, en faisant un dessin ?

[tournesol]

sais tu que G = ker p et F =im p et que p/F=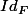
On est pas obligé de faire un dessin pour trouver une base simple de G . Son équation x=z suffit .

[GaBuZoMeu]

Un vecteur de F est de la forme (2k,k,k).
Un vecteur de G est de la forme (u,v,u).

Soit maintenant (x,y,z) un vecteur quelconque de R³. On cherche à écrire (x,y,z) sous la forme un vecteur de F + un vecteur de G. La composante sur F sera le projeté du vecteur (x,y,z) sur F parallèlement à G.

PS. Un peu plus directement : soit toujours (x,y,z) un vecteur quelconque de R³. On cherche un vecteur (2k,k,k) de F tel que la différence (x,y,z) - (2k,k,k) soit dans G, c.-à-d. ait sa troisième coordonnée égale à sa première.