Projecteurs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 20 Sep 2010, 23:19
par mehdi-128 » 20 Sep 2010, 23:19
Bonsoir, je bloque sur la démonstration de l'équivalence suivante :
Soit E un R ev. On considère 2 endomorphismes u et v de E. Montrer l'équivalence suivante :
1) uov=u et vou=v
2) u et v sont des projecteurs ayant le même noyau
J'ai essayé de montrer 2=>1
Je suis parti de u et v sont des projecteurs donc : uou=u et vov=v et Ker(u)=Ker(v)
Mais après je bloque...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Sep 2010, 23:43
par Nightmare » 20 Sep 2010, 23:43
Salut,
u et v étant des projecteurs,
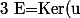\oplus Im(u)=Ker(u)\oplus Im(v))
et même chose en remplaçant Ker(u) par Ker(v) puisqu'ils sont égaux.
Soit x dans E, il se décompose au choix en
)
avec
=Ker(v))
et v(z) dans Im(v) ou en
)
.
-
=uov(y)+uovov(z)=0+uov(z)=uov(z)=u(x))
car y est dans le noyau de v et u et vov=v
-
=vou(y')+vouou(z')=0+vou(z')=vou(z')=v(x))
.
On a bien ce qu'on voulait.
Le cas 1 => 2 est quasiment évident.
:happy3:
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
 par euler21 » 20 Sep 2010, 23:49
par euler21 » 20 Sep 2010, 23:49
Bonsoir
Pour cette implication tu dois montrer que
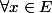
tu as uov(x) =u(x).
le principe c'est de partir de v(x)=(v(x)-x)+x
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 21 Sep 2010, 00:28
par mehdi-128 » 21 Sep 2010, 00:28
Nightmare a écrit:Salut,
u et v étant des projecteurs,
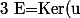\oplus Im(u)=Ker(u)\oplus Im(v))
et même chose en remplaçant Ker(u) par Ker(v) puisqu'ils sont égaux.
Soit x dans E, il se décompose au choix en
)
avec
=Ker(v))
et v(z) dans Im(v) ou en
)
.
-
=uov(y)+uovov(z)=0+u(z)=u(z)=u(x))
car y est dans le noyau de v et u et vov=v
-
=vou(y')+vouou(z')=0+v(z')=v(z')=v(x))
.
On a bien ce qu'on voulait.
Le cas 1 => 2 est quasiment évident.
:happy3:
Pour la 2 je pars de :
uov=u et vou=v
Donc : uovou=v et la je sais plus quoi faire ...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 21 Sep 2010, 00:55
par mehdi-128 » 21 Sep 2010, 00:55
Je crois qu'il y a une erreur ici :
-
=uov(y)+uovov(z)=0+u(z)=u(z)=u(x))
car y est dans le noyau de v et u et vov=v
C'est plutôt :
=uov(y)+uovov(z)=0+uov(z)=uov(z)=u(x))
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Sep 2010, 11:23
par Nightmare » 21 Sep 2010, 11:23
Oui tu as tout a fait raison, coquille corrigée !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Sep 2010, 12:04
par Nightmare » 21 Sep 2010, 12:04
Comme je l'ai dit, le cas 1=>2 n'est vraiment pas difficile :
Si x est dans le noyau de u, alors v(x)=vou(x)=v(0)=0 donc x est dans le noyau de v est vice versa par symétrie des rôles.
En plus, uou=(uov)ou=uo(vou)=uov=u et même chose pour v encore par symétrie des rôles!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
et même chose en remplaçant Ker(u) par Ker(v) puisqu'ils sont égaux.
avec
et v(z) dans Im(v) ou en
.
car y est dans le noyau de v et u et vov=v
.
