Produit cartésien et puissance du continu

[Groomy26]

Bonsoir,

Pouvez-vous m'aider sur la démonstration de la propriété suivante :

Si A et B sont deux ensembles à la puissance du continu, alors le produit cartésien AxB est aussi à la puissance du continu.

Dans l'attente de recevoir vos pistes de recherches, bien cordialement

[Ben314]

Salut,
Par hypothèse, A et B sont en bijection avec R donc avec ]0,1[ et ça signifie que AxB est en bijection avec ]0,1[^2.
Il suffit donc de montrer que ]0,1[^2 est en bijection avec ]0,1[.
Si on prend un couple (x,y) de ]0,1[^2, qu'on les écrit sous forme décimale x=0,x1x2x3... ; y=0,y1y2y3... (en prenant l'écriture propre, c'est à dire celle se terminant par une suite de 0 pour les nombres décimaux qui ont deux écriture) et qu'on lui associe le nombre z=0,x1y1x2y2x3y3... cela fournit une injection de ]0,1[^2 dans ]0,1[ (*)
Réciproquement, l'application x->(x,1/2) fournit une injection de ]0,1[ dans ]0,1[^2.
Le théorème de Cantor-Bernstein permet alors de conclure.

(*) Pourquoi est-ce une injection ? Est-ce une bijection ?

[Groomy26]

Salut,

D'abord, merci beaucoup pour votre aide qui s'est montré très claire !

Pour démontrer que il s'agit d'une injection, j'ai procédé comme suit (je suis revenu à la définition d'application injective) :



Soient tels que ont pour écriture propre respectives : et .



Par unicité du développement décimal assuré par l'écriture propre de, on obtient :
.

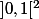Ainsi est une injection de sur .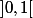

Cela est-il correct ?

[Ben314]

Oui, sur le principe, c'est "à peu prés" bon, mais à mon avis, tu ne pointe pas assez du doigt LE point qui à mon avis est le point essentiel de la preuve, à savoir que si on prend l'écriture propre de x et de y, alors l'écriture 0,x1y1x2y2.... est elle même une écriture propre.
Et c'est parce que les deux écritures 0,x1y1x2y2.... et 0,x'1y'1x'2y'2.... sont toute les deux propres (et qu'elle représentent le même réel) que tu peut en déduire que les chiffres qui les composent sont les même.
(et a mon avis, il faut aussi dire un petit truc concernant le fait que, si x et y sont dans ]0,1[ alors 0,x1y1x2y2.... est lui aussi dans ]0,1[, en particulier expliquer qu'il ne peut pas être égal à 0,9999... qui vaut 1)

Et c'est d'autant plus important que c'est faux dans l'autre sens, c'est à dire que si 0,x1y1x2y2.... est une écriture propre, ça ne prouve pas que 0,x1x2x3... et 0,y1y2y3... sont elle même propres. Et c'est pour ça que la fonction n'est pas surjective (donc pas bijective) : le réel 0,352929292929... n'a pas d'antécédent vu que son seul antécédent potentiel, c'est le couple (x,y) avec x=0,32222... et y=0,59999... sauf que l'écriture propre de y, c'est y=0,60000... et pas y=0,5999... donc ça marche pas.