Problème sur les restes !!!!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par sandrine_guillerme » 23 Oct 2006, 00:15
Bonsoir Tout le monde .
J'ai encore des petites soucies sur les Restes (mes la c'est sur les séries) .. il s'agit de deux question en fait .. voici le problème en entier ..
^n a_n(x))
avec
 = \frac{x^2+n}{n^2})
a/ pour x fixé montrer que la série
converge simplement
(ça j'ai fais)b/
absoument cv ?
(sa j'ai fais)c/ Soit
le reste d'ordre N de
prouver que pour tout x réel \Large
|\le a_{N+1})
(ça j'ai fais).en déduire que si X est une partie bornée la séries
converge uniformément ?
(j'ai pas fais ça ) d/ prouver que pour tout x dans R
 \ge a_{N+1}(x) - a_{N+2}(x))
et en déduire que lim quand N tend vers
La convergence de [v_n] est elle uniforme ?
(j'ai pas fais la d non plus 
) Merci de m'aider .
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 23 Oct 2006, 01:00
Salut sandrine,
sur une partie bornée
(par exemple
) on a:
]-[v_n(x)]\|=sup\limits_{x\in B}|R_n(x)|\leq sup\limits_{x\in B}a_{n+1}(x)=sup\limits_{x\in B}\frac{x^2+n+1}{(n+1)^2}\leq \frac{M^2+n+1}{(n+1)^2}\;\longrightarrow\limits_{n\to\infty}\;0)
par sandrine_guillerme » 23 Oct 2006, 08:20
Excusez moi, mais je me permes de faire remonter le sujet .. queqlqu'un pour me sauver SVP?
par sandrine_guillerme » 23 Oct 2006, 10:39
Y aurai t il quelqu'un pour m'aider a faire la question d/ svp ?
Merci :triste:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 23 Oct 2006, 11:22
Salut Sandrine,
pour la d) j'ai pas bien compris ce que tu as écris... tu veux montrer que
\|\geq a_{n+1}(x)-a_{n+2}(x))
c'est bien ça exactement avec des valeurs absolue non ?
=\sum\limits_{k=n+1}^{\infty}(-1)^ka_k(x))
et
\)_k)
est une suite décroissante...
par sandrine_guillerme » 23 Oct 2006, 11:31
Comment ceci achève la démonstration ? et si c'est une suite décroissante comment la limite de R_n(n^2) va tendre vers + l'infini c'est plutot - linfini ... ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 23 Oct 2006, 11:41
Si on détail beaucoup, ça fait ça (tout vient de la decroissance de
et du
^n)
) :
si (n+1) est pair :
Donc
\geq a_{n+1}(x)-a_{n+2}(x)>0)
(on peut mettre des valeurs absolue à
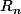
, il est positif, ça ne change rien...)
si (n+1) est impair :
=-a_{n+1}(x)+a_{n+2}(x)+\underbrace{R_{n+2}(x)}_{0)
Donc dans tous les cas (pair, impair) :
\|\geq a_{n+1}(x)-a_{n+2}(x))
par sandrine_guillerme » 23 Oct 2006, 11:47
Oups :id: Je vois mieux là .. Un grand bravo et un grand merci José ..
Bonne journée .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
