Problème sur les restes .

[sandrine_guillerme]

Salut tout le monde ,

Je suis de retour avec un nouveau problème sur les restes ..
montre que la série de terme général v_n = 1/(3^n)+1 n entier natuel est convergente (ça j'ai fais )

soit V sa somme V_n = somme de k=0 à n (v_k) et R_n = V-V_n
majorer R_n
j'ai essayer de le comparer avec 1/3^n+1 (la série géométrique) .. mais je ne sais pas comment avancer ..

quelqu'un pour m'aider svp ?
Merci d'avance .

[tize]

Salut Sandrine,

donc .
Donc

[sandrine_guillerme]

Merci José ..

donc la je trouve


j'ai majoré le reste par un terme qui tend vers 0 ..

C'est bon?

[tize]

Merci José ..

donc la je trouve


j'ai majoré le reste par un terme qui tend vers 0 ..

C'est bon?

attention aux indices, la somme commence à n+1 et tu peux calculer cette série...

[sandrine_guillerme]

Et si c'est bon .. je me propose la suite suivante

et son reste ( il est défini bien sur vu que la suite converge absolument .
donc je veux majorer le ..


ça tend aussi vers 0 c'est une bonne majoration je sens qu'il y a quelque chose qui cloche la ?

[sandrine_guillerme]

Excuse moi j'ai pas actualisé ..



C'est bon?

[tize]

Attention à ce que tu écris.

et donc :

[sandrine_guillerme]

Oui ok Je vois mieux la regardons maintenant ça de plus près .. :/

.. je me propose la suite suivante

et son reste ( il est défini bien sur vu que la suite converge absolument .
donc je veux majorer le ..

on peut pas le majorer par car il n'y pas de relation d'ordre .. ?
ça tend aussi vers 0 Selon la forme réduite du théorème d'Abel .. Correct ?

[sandrine_guillerme]

C'est juste pour faire remonter ce message .. Je sais pas si tu as actualisé José .. Merci beaucoup d'avance .

[tize]

C'est juste pour faire remonter ce message .. Je sais pas si tu as actualisé José .. Merci beaucoup d'avance .

Oui, oui, ne t'en fais pas, j'actualise assez souvent (sauf quand je ne suis pas là)...tu as compris ? as-tu encore une question ? (n'hesites pas)

[sandrine_guillerme]

Oui j'ai compris merci bien de me soutenir ,et pour éviter les multipost regarde ce que j'ai ecris juste avant de faire remonter le message

[tize]

Si tu parles de ton message #8, la valeur absolue de est 1

[sandrine_guillerme]

j'ai cru que je l'avais écris oh zut.. ! excuse moi José .. :/

je veux plutôt déterminer le plus petit entier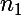 tel que l'on obtienne par cette majoration

Donc la j'ai essayer dans tout les sens ..
mais je ne vois pas trop comment faire
Voila ce que j'ai fais :

j'ai essayer pour certaine valeurs de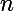
par exemple pour je trouve

mais c'est pas vraiment ce que je cherche :triste:
que faire ?

[tize]

C'est une série alternée décroissante en valeur absolue,
C'est que tu veux majorer ou ? Car change de signe tout le temps ...

[sandrine_guillerme]

je parle de la valeur absolue ...

[tize]

Je pense que c'est ...
Remarque bien que la suite est décroissante en valeur absolue et aussi alternée. On peut donc majorer directement par le premier terme en valeur absolue c'est à dire .
Il ne reste qu'à résoudre :

[sandrine_guillerme]

Ah ok !!!!!
c'est mailin ça !! Je vais essayer d'avancer sur le probleme .. Il est très long .. Je te l dirais si probleme .. Merci Beaucoup !!!

[sandrine_guillerme]

comme prévu j'ai un petit souci là ..

et soit sa somme et

Montrer que U_2p est décroissante .. je ne sais pas c'est quoi qu'il faut caclculer peut être si oui j'ai du mal .. parceque je ne suis pas trop "indices" moi :'(

aide moi stp?

[tize]

c'est une suite dont les termes sont tous positifs et évidement décroissante puisque le dénominateur croit avec ...

[sandrine_guillerme]

Merci ,

Mais en fais l'exerice parle de et non devrais je la considèrer comme erreur?