Problème sur les restes .

par **tize** » 22 Oct 2006, 13:01

a d'accord,

c'est ça ?

par **sandrine_guillerme** » 22 Oct 2006, 13:06

Exactement .. que me propose tu ?

par **tize** » 22 Oct 2006, 13:13

reste à montrer que c'est négatif...

par **sandrine_guillerme** » 22 Oct 2006, 14:11

ok d'accord .. ensuite on me demande de montrer que

ça je l'ai fais selon ton indication .. et que

a pour limite 0 . ça je l'ai fais aussi .

puis montrer que les deux suites sont adjacentes qu'ils ont une limite commune et qui vérifie pour tout entier naturel p

ça je l'ai fais aussi.

Donc l'avant dernière question c'est de déterminer leplus petit entier

tel que

Comment faire ?

[Edit] : Je rajoute que

c'est la somme de

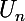qui est la série de terme général

.

par **tize** » 22 Oct 2006, 14:28

donc comme il y a alternance et decroissance en valeur absolue, on peut majorer par le premier terme:

à résoudre ...

par **sandrine_guillerme** » 22 Oct 2006, 14:40

Ah ok .. Je vois .. Merci beaucoup José . c'est vraiment bien aimable .

Problème sur les restes .

Qui est en ligne