Problème de proba
Problème de proba
Bonjour qlq peut m’aider à faire cette exo
Une petite productrice fabrique des plaques de chocolat bio. Lorsque les paramètres de sa machine sont bien réglés, on considère que le poids d’une plaque choisie au hasard est une variable aléatoire X qui suit une loi normale de moyenne m0 = 201g et de variance σ0^2= 4.
Pour vérifier si la machine fonctionne bien, la productrice effectue régulièrement des pesées de n plaques de chocolat sélectionnées au hasard soit Xi avec i compris entre 1 et n le poid de la i-eme plaque prélevé
On pose Xnbarre=1/n fois la somme des Xi Pour i=1 a n
Xnbarre ^2= 1/n fois la somme des Xi^2 pour i=1 a n
Sn^2=1/n-1 fois la somme de (Xi-Xnbarre)^2
On suppose que les Xi sont indépendantes et de même loi normale de paramètres m et σ ^2. On
admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté.
1. Donner la loi de Xnbarre
2. Montrer que Xnbarre est un estimateur sans biais et consistant de m
Une petite productrice fabrique des plaques de chocolat bio. Lorsque les paramètres de sa machine sont bien réglés, on considère que le poids d’une plaque choisie au hasard est une variable aléatoire X qui suit une loi normale de moyenne m0 = 201g et de variance σ0^2= 4.
Pour vérifier si la machine fonctionne bien, la productrice effectue régulièrement des pesées de n plaques de chocolat sélectionnées au hasard soit Xi avec i compris entre 1 et n le poid de la i-eme plaque prélevé
On pose Xnbarre=1/n fois la somme des Xi Pour i=1 a n
Xnbarre ^2= 1/n fois la somme des Xi^2 pour i=1 a n
Sn^2=1/n-1 fois la somme de (Xi-Xnbarre)^2
On suppose que les Xi sont indépendantes et de même loi normale de paramètres m et σ ^2. On
admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté.
1. Donner la loi de Xnbarre
2. Montrer que Xnbarre est un estimateur sans biais et consistant de m
Modifié en dernier par mathieu426 le 12 Avr 2020, 01:51, modifié 3 fois.
Re: Problème de proba
Bonjour,
Du cours :
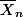 est la moyenne empirique des
est la moyenne empirique des 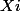
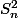 est la variance empirique de l'échantillon des
est la variance empirique de l'échantillon des 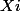
La question 1 est une question de cours. Qu'avez-vous répondu?
Du cours :
La question 1 est une question de cours. Qu'avez-vous répondu?
Re: Problème de proba
Xnbarre est une loi normale N(m, σ^2/n)
X suit une loi normale X1......Xn est un échantillon aléatoire de loi N(m, σ^2)
Les plaques de chocolat choisit au hasard donc c un échantillon aléatoire et d’après l’énoncé Xi indépendants et de loi normale alors Xnbarre suit une loi normale
Donc
Xnbarre est une loi normale N(m, σ^2/n)
2) E(Xnbarre)=E(X1+........+Xn)/n=nm/n=m
Donc Xnbarre est un estimateur sans biais
Pour la variance
Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n
=n σ^2/n^2= σ^2/n
L’estimateur est sans biais est sa variance tend vers 0 il est donc consistant
X suit une loi normale X1......Xn est un échantillon aléatoire de loi N(m, σ^2)
Les plaques de chocolat choisit au hasard donc c un échantillon aléatoire et d’après l’énoncé Xi indépendants et de loi normale alors Xnbarre suit une loi normale
Donc
Xnbarre est une loi normale N(m, σ^2/n)
2) E(Xnbarre)=E(X1+........+Xn)/n=nm/n=m
Donc Xnbarre est un estimateur sans biais
Pour la variance
Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n
=n σ^2/n^2= σ^2/n
L’estimateur est sans biais est sa variance tend vers 0 il est donc consistant
Modifié en dernier par mathieu426 le 11 Avr 2020, 22:50, modifié 3 fois.
Re: Problème de proba
Bonjour,
êtes-vous sur que Xnbarre ^2= 1/n fois la somme des Xi^2 pour i=1 a n (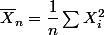 ) et pas
) et pas 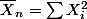
êtes-vous sur que Xnbarre ^2= 1/n fois la somme des Xi^2 pour i=1 a n (
Re: Problème de proba
Bonjour,
Quand utilisez-vous : On admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté.
Quand utilisez-vous : On admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté.
Re: Problème de proba
Oui 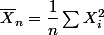
Et (n − 1)Sn^2/σ^2 est utile pour les questions 3 et 4
Et (n − 1)Sn^2/σ^2 est utile pour les questions 3 et 4
Modifié en dernier par mathieu426 le 12 Avr 2020, 00:25, modifié 1 fois.
Re: Problème de proba
Bonjour,
Ok. Je ne vois pas tout l'exercice. Donc parfois je vous pose des questions hors contexte.
Sinon , on est bien d'accord il y un carrée sur le Xnbarre(je l'avais oublié)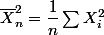
Ok. Je ne vois pas tout l'exercice. Donc parfois je vous pose des questions hors contexte.
Sinon , on est bien d'accord il y un carrée sur le Xnbarre(je l'avais oublié)
Re: Problème de proba
Bonjour,
pour Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n c'est faux car Var(aY)= tex]a^2 Var(Y)[/tex]
Rappelez-vous que la variance est non linéaire vous devriez avoir un tex]\frac{1}{n^2 Var(Y)[/tex], c'est sans doute une erreur de frappe de votre part.
Sinon cela me semble correcte par apport aux éléments que vous m'avez fournis
pour Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n c'est faux car Var(aY)= tex]a^2 Var(Y)[/tex]
Rappelez-vous que la variance est non linéaire vous devriez avoir un tex]\frac{1}{n^2 Var(Y)[/tex], c'est sans doute une erreur de frappe de votre part.
Sinon cela me semble correcte par apport aux éléments que vous m'avez fournis
Re: Problème de proba
Bonjour,
Erratum : je refais une partie de mon dernier post à cause de Latex erreur
pour Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n c'est faux car Var(aY)=)
Rappelez-vous que la variance est non linéaire vous devriez avoir un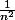 au lieu de
au lieu de 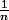
Erratum : je refais une partie de mon dernier post à cause de Latex erreur
pour Var(Xnbarre)=var(X1.........Xn)/n=var(X1).......+var(Xn)/n c'est faux car Var(aY)=
Rappelez-vous que la variance est non linéaire vous devriez avoir un
Re: Problème de proba
Montrer que Snˆ2 est un estimateur sans biais et consistant
Je commence par trouver que Sn^2=n(Xn^2barre -(Xnbarre)^2)/n-1
Mais je n’arrive pas à montrer que c’est un estimateur sans biais
E(Sn^2)=E(Xn^2barre -Xnbarre^2)/n-1)=(1/n-1)(E(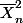 )-E(
)-E(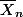 ^2)
^2)
Je remplaceE(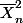 )Par 1/nE(
)Par 1/nE(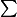
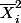 ) et E(
) et E(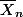 ) par (1/n)E(
) par (1/n)E(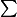
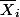 )
)
On a donc 1/nE(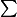
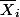 )=E(
)=E(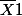 )......+ E(
)......+ E(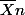 )/n=nm/n=m
)/n=nm/n=m
Et (1/n)E(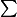
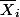 ) donne
) donne
E( ........ E(
........ E( 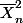 )/n=n
)/n=n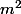 /n=
/n=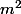
Je ne vois pas quoi faire à partir de là car je trouve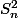 =0
=0
Je pense qu’il faut utiliser On
admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté mais je vois pas comment faire
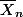
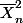
Je commence par trouver que Sn^2=n(Xn^2barre -(Xnbarre)^2)/n-1
Mais je n’arrive pas à montrer que c’est un estimateur sans biais
E(Sn^2)=E(Xn^2barre -Xnbarre^2)/n-1)=(1/n-1)(E(
Je remplaceE(
On a donc 1/nE(
Et (1/n)E(
E(
Je ne vois pas quoi faire à partir de là car je trouve
Je pense qu’il faut utiliser On
admettra que (n − 1)Sn^2/σ^2 suit une loi du chi-deux à n − 1 degrés de liberté mais je vois pas comment faire
Re: Problème de proba
Bonjour,
Je croyais que la question était :"Montrer que Snˆ2 est un estimateur sans biais et consistant "
Je croyais que la question était :"Montrer que Snˆ2 est un estimateur sans biais et consistant "
Re: Problème de proba
oui la question d'après celle que je n'arrive pas à faire
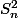 je le trouve en développent le
je le trouve en développent le ^2)
J’obtiens (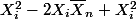 )
)
Ensuite )
)
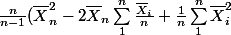 )
)
J’obtiens (
Ensuite
Modifié en dernier par mathieu426 le 12 Avr 2020, 14:06, modifié 13 fois.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
