Probleme étude d'une serie numerique.

par **JGGJ** » 01 Juil 2009, 16:46

bonjour tout le monde,
je sollicite votre aide pour me donnée une petit idée, et ou la démarche a suivre pour l'étude, concernant de la convergence d'une série numérique.

sin (

)

j'ai essayé de voulais appliquer la règle de Cauchy mais il y a le sin qui me gène. j'ai penser a l'équivalence mais la encore le sinus me pose problème.

merci pour tout aide.

par **fatal_error** » 01 Juil 2009, 17:19

salut,

sauf erreur, le terme dans le sinus tend vers 0. Tu peux donc faire un equivalent sin(x) ~ x quand x tend vers 0, soit quand n tend vers l'infini.
Il reste apres plus qu'a appliquer le lemme d'abel.

par **busard_des_roseaux** » 01 Juil 2009, 17:33

fatal_error a écrit:salut,

sauf erreur, le terme dans le sinus tend vers 0. Tu peux donc faire un equivalent sin(x) ~ x quand x tend vers 0, soit quand n tend vers l'infini.
Il reste apres plus qu'a appliquer le lemme d'abel.

re,

il convient de pousser le DL du sinus, jusqu'à obtenir
des termes de séries absolument convergentes, ie, jusqu'à l'ordre 3.

Elle converge mais pas absolument.

par **fatal_error** » 01 Juil 2009, 17:40

pourquoi faut-il la convergence absolue?

C'est un "critère" pour les equivalences?
En plus perso, j'aurais dit qu'elle convergeait uniformément, grace au lemme d'abel.

Si tu peux eclairer ma lanterne...merci :-)

par **kazeriahm** » 01 Juil 2009, 18:06

attendez, soit j'hallucine, soit le terme général equivaut à 2*(-1)^n/sqrt(n), , qui définit bien une série convergente selon le "critère des séries alternées"

pourquoi pousser le DL ?

fatal_error la convergence uniforme n'a de sens que pour une série de fonctions il me semble

par **nuage** » 01 Juil 2009, 18:14

Salut,

je ne vois pas pourquoi vous parlez de convergence uniforme : il ne s'agit pas d'une série de fonction.
De plus elle n'est pas absolument convergente.

Par contre on peut appliquer le critère de convergence des séries alternées :
pour n assez grand, et il est vite assez grand,

tend vers zéro en décroissant.

[edit] doublé par kazeriahm

par **fatal_error** » 01 Juil 2009, 18:21

erf si je commence a confondre le peu que j'ai appris...

je voulais utiliser le fait qu'on ait une fonction decroissante avec une fonction alternée, bref, un bon cafouillis made in moi =)

par **busard_des_roseaux** » 01 Juil 2009, 18:41

kazeriahm a écrit:attendez, soit j'hallucine, soit le terme général equivaut à 2*(-1)^n/sqrt(n), , qui définit bien une série convergente selon le "critère des séries alternées"

pourquoi pousser le DL ?

les termes sont équivalents mais les séries pas de même nature,
à cause du terme d'ordre suivant en

dans le DL

par **kazeriahm** » 01 Juil 2009, 18:47

bien vu bien vu, en fait il faut que les deux termes soient de signe constant pour que le resultat (u_n equivaut a v_n) implique (somme(u_n) de meme nature que somme(v_n)) soit vrai

par **JGGJ** » 01 Juil 2009, 19:14

nuage a écrit:Salut,

je ne vois pas pourquoi vous parlez de convergence uniforme : il ne s'agit pas d'une série de fonction.
De plus elle n'est pas absolument convergente.

Par contre on peut appliquer le critère de convergence des séries alternées :
pour n assez grand, et il est vite assez grand, tend vers zéro en décroissant.

[edit] doublé par kazeriahm

utiliser le théorème fondamental des séries alternées me parait plus correcte
mais la le terme générale tende vers 0 en décroissant mais on sais pas si c 'est en valeur absolus.?

par **nuage** » 03 Juil 2009, 21:08

Salut,
je suis désolé de m'être aussi mal exprimé.
Il est immédiat que

et que

.
Pour

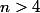
on a

,
La fonction sinus est croissante sur

donc

est une fonction décroissante de

.
La série est donc convergente.

Il est important de remarquer qu'elle n'est pas absolument convergente.

Probleme étude d'une serie numerique.

probleme étude d'une serie numerique.

Qui est en ligne