Probleme egalité analyse numerique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 30 Oct 2008, 18:57
par muse » 30 Oct 2008, 18:57
Bonjour,
voila j'ai encore une fois un problème .

Je n'arrive pas à montrer qu'il existe un c mais j'arrive a le trouver.
Voila ce que j'ai fait en cherchant:
En fait je calcule
=f(x)-p_1(x)-Ax(x-a))
Et je dis que on choisit A de telle manière a ce que c soit racine de g
On trouve donc c assez facilement.
En appliquant deux fois Rolles à g je trouve qu'il existe un c telle que g''(c)=0 et que A= \frac{f''(c)}{2}
j'ai donc:
-p_1(c)=\frac{f''(c)}{2}c(c-a))
Mais c'est pas ce qu'on veut...
Mais j'ai des doutes j'ai l'impression que le c de f''(c) n'est pas le même que les autres c.
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 30 Oct 2008, 20:59
par muse » 30 Oct 2008, 20:59
le polynome d'interpolation de legenre il est facile a trouver c'est une fonction affine linaire qui est a²x
Le problème c'est l'égalité

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 30 Oct 2008, 21:09
par Sa Majesté » 30 Oct 2008, 21:09
OK pour p1(x)=a²x
L'existence de c est donnée par Taylor-Young
Pour déterminer c, il suffit d'écrire (puisque f"(c)=6c)
x^3 - a²x = 3c x (x-a)
x (x-a) (x+a)= 3c x (x-a)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 30 Oct 2008, 22:45
par muse » 30 Oct 2008, 22:45
Ok j'avais mal lu.
Mais je pense qu'il faut faire la démonstration dans ce cas la et pas juste citer taylor youn.
Donc en fait la on ecrit
= p_1(x) + Ax(x-a))
Donc ce qu'on fait en fait c'est qu'on fait une nouvelle approximation mais par un polynome de degrés 2, on ajoute donc une nouvelle racine qu'on nomera k (on peut trouver a en de maniere a ce que k soit racine)
y'a plus qu'a démontrer que il existe c tel que
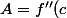}{2})
Pour ça on prend
=f(x)- p_1(x) + Ax(x-a))
donc g(x) s'annule en 0,k,a par 2 application de Rolles de suites on en déduit qu'il existe c tel qu'on g''(c)=0=f''(c)+2A= donc
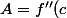}{2})
Je pense que c'est bon
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités

