ok, y a du taf.
Les polynômes de Tchebycheff sont des polynômes de degré n
vérifiant:
=T_n(cos(x)))
c'est aussi simple que cela, ça vient des formules d'Euler.
On a donc:
- une formule trigo explicite pour leurs racines
- une relation de récurrence
- ils constitutent une famille orthogonale pour le produit scalaire
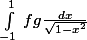
et une base de l'e.v
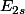
des polynomes de degré au plus 2s-1,
e.v de dimension 2s.
ta formule à démontrer
 \frac{dx}{\sqrt{1-x^2}}=\frac{\pi}{s} \sum_{m=1}^{s} f(c_m))
n'est rien d'autre que
l'égalité de deux formes linéairesdéfinie sur l'e.v
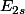
On la vérifie donc sur une base de l'e.v, celle de Tchebycheff.
Pour un polynôme
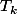
, il vient à gauche:
 \frac{dx}{\sqrt{1-x^2}}=<br />\int_{0}^{\pi} T_k(cos(u)) du=\int_{0}^{\pi} cos(ku) du=0)
si
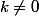
et

sinon.
voilà pour le membre de gauche de l'égalité.
Pour celui de droite,
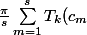<br />=\frac{\pi}{s} \sum_{m=1}^{s} T_k(\cos(\frac{(2m-1)\pi}{2s})<br />=\frac{\pi}{s} \sum_{m=1}^{s} \cos(\frac{k(2m-1)\pi}{2s}))
cette dernière somme
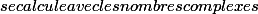
en remarquant que c'est la partie réelle d'une progression géométrique,
formée avec des exponentielles.
je te laisse terminer la vérification.

