re,
je plussoie. Sachant
)=cos(nx))
on a bien:
 \frac{dx}{\sqrt{1-x^2}}=0)
si n >0 et

si n=0
Pour l'autre membre, si k>0 :
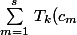=\frac{\pi}{s} \sum_{m=1}^{s}<br />\, \cos(\frac{k(2m-1)\pi}{2s}))
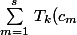=\frac{\pi}{2s} 2 \Re \left( \sum_{m=1}^{s} \, e^{ik(2m-1) \frac{\pi}{2s}} \right))
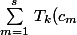=\frac{\pi}{s} \Re \left( e^{ik \frac{\pi}{2}} \frac{\sin(\frac{k \pi}{2})}{\sin(\frac{k\pi}{2s})}\right))
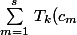=\frac{\pi}{2s} \frac{\sin(k \pi)}{\sin(\frac{k\pi}{2s})}=0) quelques remarques sur
quelques remarques sur \frac{dx}{\sqrt{1-x^2}}=\frac{\pi}{s} \sum_{m=1}^{s} f(c_m))
1) il s'agit bien de deux formes linéaires, définies sur l'e.v des fonctions
continues sur [-1,1]
2) cette égalité s'annule, à gauche de l'égalité, pour f, polynôme de Tchebycheff de degré n quelconque >0.
Cette égalité est surprenante:
la forme linéaire , à gauche, admet
tous les polynômes de Tcheby dans son noyau.
La forme linéaire de droite est décrite de la manière suivante:
soit
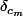
la masse de Dirac en
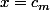
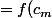)
La forme linéaire de droite est une moyenne pondérée de masse de Dirac
aux points
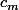
, pour

zéros du polynôme
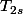
moyenne étendue à s éléments.
Elle, a-priori, elle a
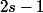
polynômes de Tcheby dans son noyau.
Tu devrais pouvoir interpréter ta quadrature comme une convergence
d'opérateurs relativement à la topologie duale faible-* ????
malheureusement, je connais pas. L'idée, c'est que l'on moyenne
de plus en plus de masses de Dirac. Et le support de cette moyenne de mesures de Dirac devient dense sur [-1;1].
En gros, ce sont les mesures qui "convergent", en moyenne de Césaro, testées sur des fonctions intégrandes, qui, elles, sont "fixes".
Ce qu'il faudrait voir, c'est comment se comporte cette suite de noyaux,
pour les formes linéaires du membre de droite, quand s tend vers l'infini.
Obtient une suite exacte ? Est-ce une "limite projective" ?
