Soit z= (1+2ik)/(1-2ik), k un entier
Il faut montrer que z n'est pas une racine nieme de l'unité
Pour le montrer, j'ai fait un raisonnement par l'absurde donc jai supposé que z etait une racine niem de l'unité
de la, jai deduit la relation (1+2ik)^n =(1-2ik)^n
Mais après je suis bloqué, je ne vois plus quoi faire
Si vous avez une ptite idée , merci de m'aider ! :we:
Probleme avec racine nieme de l'unité
4 messages
- Page 1 sur 1
oui mais on a pas (1+2ik)=(1-2ik) ! on a (1+2ik)^n=(1-2ik)^n
donc ce que tu dis n'est pas bon
j'ai oublié de le dire, mais je sais qu'on doit arriver a un moment a la conclusion que 1+4k² divise 2^m * k² (m un reel ) et qu'il ya semble t'il besoin des modules pour y arriver ( en effet , 1- 2ik est le conjugué de 1+2ik et on sait z*z(barre)= mod(z)² soit ici, mod(z)²=1+4k²)
donc ce que tu dis n'est pas bon
j'ai oublié de le dire, mais je sais qu'on doit arriver a un moment a la conclusion que 1+4k² divise 2^m * k² (m un reel ) et qu'il ya semble t'il besoin des modules pour y arriver ( en effet , 1- 2ik est le conjugué de 1+2ik et on sait z*z(barre)= mod(z)² soit ici, mod(z)²=1+4k²)
Bonjour,
j'ai bien une solution mais qui utilise un argument plus simple que celui que tu indiques. Il est possible que je me trompe mais ne vois pas la faille:
Je continue sur ton idée^n = (1 - ik)^n) signifie que
signifie que ^n) est réel (c'est toujours le cas quand un complexe est égal à son conjugué
est réel (c'est toujours le cas quand un complexe est égal à son conjugué
Cela signie que sa partie imaginaire est nulle
Cela signifie que
^p=0)
Soit encore(en divisant par 2ik)
^{p-1 \over 2}=0)
on remarque que,si k est non nul, pour être nulle cette somme doit comporter au moins deux termes donc que n est supérieur ou égal à 3
D'autre part on sait que
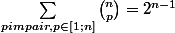
En faisant la différence des deux égalités
^{p-1 \over 2}) = 2^{n-1})
le terme pour p = 1 est nul,donc
^{p-1 \over 2}) = 2^{n-1})
Or, dans^{p-1 \over 2})) on peut mettre
on peut mettre 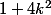 en facteur (identité remarquable)
en facteur (identité remarquable)
donc^{p-1 \over 2})) est divisible par
est divisible par 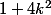
donc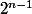 est divisible par
est divisible par 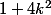
impossible pour k non nul
donc égalité de départ impossible
j'ai bien une solution mais qui utilise un argument plus simple que celui que tu indiques. Il est possible que je me trompe mais ne vois pas la faille:
Je continue sur ton idée
Cela signie que sa partie imaginaire est nulle
Cela signifie que
Soit encore(en divisant par 2ik)
on remarque que,si k est non nul, pour être nulle cette somme doit comporter au moins deux termes donc que n est supérieur ou égal à 3
D'autre part on sait que
En faisant la différence des deux égalités
le terme pour p = 1 est nul,donc
Or, dans
donc
donc
impossible pour k non nul
donc égalité de départ impossible
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
