Problème d'arithmétique

[hussein515]

Bonjour à toutes/tous,

Je dois résoudre le problème suivant:

Soit , , trois entiers naturels deux à deux premiers entre eux. Montrer que l'ensemble , des entiers , tels que admet un plus petit élément .

Je propose la solution suivante:

Les nombres , et , sont premiers entre eux donc la suite est périodique de période ,. On a:



De même, , et , étant premiers entre eux, la suite est périodique de période , et . Il en résulte



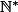ce qui prouve: . Donc , partie non vide de possède un plus petit élément .

Mais ma solution n'utilise pas l'hypothèse du début à savoir (puisque les trois entiers sont supposés être deux à deux premiers entre eux. J'ai donc dû faire une erreur qque part mais je ne vois pas où. Si vous voyez l'erreur, dites le moi svp !

Merci !

hussein

[Rdvn]

Bonsoir

Votre réponse me semble correcte
Moi non plus je ne vois pas d’utilité à l'hypothèse " a et b premiers entre eux"
il y avait aussi la solution évidente r=s= phi(m) indicatrice d'Euler

Qu'en pensez vous ?
cordialement
Rdvn

[hussein515]

Bonsoir

Votre réponse me semble correcte
Moi non plus je ne vois pas d’utilité à l'hypothèse " a et b premiers entre eux"
il y avait aussi la solution évidente r=s= phi(m) indicatrice d'Euler

Qu'en pensez vous ?
cordialement
Rdvn

Bonsoir Rdvn,

Oui effectivement, , solution encore plus simple, bravo et merci. Donc il suffit de supposer et premiers avec uniquement. Merci pour votre réponse.

Hussein

[Rdvn]

Bonsoir
Était ce un exercice "comme ça " ou u,e partie de problème ?

[hussein515]

Bonsoir
Était ce un exercice "comme ça " ou u,e partie de problème ?

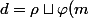Il y avait une deuxième question où l'on demande de montrer que divise , je l'ai fait assez facilement en introduisant et en utilisant le théorème de Bezout-Bachet.

A+

hussein

[Rdvn]

OK
A+
R.