Je suis bloquée dans un exercice avec la question suivante :
La variable Y s'exprime linéairement en fonction du carré de X : Y=2X²-1. En déduire la moyenne de Y en utilisant les résultats précédents.
Les résultats précédents sont E(X)=0,95 ; E(X²)=2,65 ; Var(X)=1,7475.
Comment doit je faire pour trouvée la moyenne de Y ?
Je sais que E est un opérateur linéaire donc que si j'ai Y=aX+b alors E(Y)=aE(X)+b.
Est ce que E(Y)=2E(X²)-1 ou E(Y)=2[E(X)]²-1 ????
La question qui suit est la suivante : définir la loi de probabilité de Y, puis calculer directement la moyenne de Y. La non plus je ne vois pas.
Probabilités
7 messages
- Page 1 sur 1
par Anonyme » 30 Aoû 2005, 14:21
Donc si j'ai bien compris :
Y = 2X²-1
E(Y) = 2E(X²)-1 = 2x2,65-1 = 4,3.
Et dans l'autre question : définir la loi de probabilité de Y, puis calculer directement la moyenne de Y.
Il faut que je me serve des xi pour trouver les yi (avec yi = 2xi-1) et calculer E(Y) avec la formule E(Y) = SOMME yi x pi ce qui donne aussi 4,3.
Y = 2X²-1
E(Y) = 2E(X²)-1 = 2x2,65-1 = 4,3.
Et dans l'autre question : définir la loi de probabilité de Y, puis calculer directement la moyenne de Y.
Il faut que je me serve des xi pour trouver les yi (avec yi = 2xi-1) et calculer E(Y) avec la formule E(Y) = SOMME yi x pi ce qui donne aussi 4,3.
par Galt » 30 Aoû 2005, 15:03
Est-ce que X est une variable discrète ou à densité ?
Si X est une variable discrète, elle prend les valeurs
, donc Y prend les valeurs 
. On est tenté d'écrire =p(X=x_i))
ce qui donnerait la loi, mais c'est malheureusement faux, car si X peut prendre deux valeurs opposées, alors Y predra la même valeur. En fait, l'événement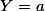 
s'écrit 
donc 
ou 
. On a donc 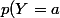=p\(X=\sqrt{\frac{a+1} 2}\)+p\(X=-\sqrt{\frac{a+1} 2}\))
(pour tout 
)
Si maintenant
suit une loi à densité f , alors l'événement 
va se traduire par 
soit 
soit 
ou 
, et donc =\int_{\sqrt{\frac{a+1} 2}}^{\sqrt{\frac{b+1} 2}}f(t)\,dt+\int_{-\sqrt{\frac{b+1} 2}}^{-\sqrt{\frac{a+1} 2}}f(t)\,dt)
(avec toujours )
Si on veut la loi de Y, on prend
et on pose =p(\frac {-1} 2\leq Y\leq b))
, ce qui donne =\int_{-\sqrt{\frac{b+1} 2}}^{\sqrt{\frac{b+1} 2}}f(x)\,dx)
, et la loi g de Y est la fonction 
, soit =\frac 1 {4\sqrt{\frac{b+1} 2}} f\(\sqrt{\frac {b+1} 2}\)+\frac 1 {4\sqrt{\frac{b+1} 2}} f\(-\sqrt{\frac {b+1} 2}\))
(si je n'ai pas fait d'erreur dans mes calculs de dérivée), et bien évidemment tout ça pour 
Si X est une variable discrète, elle prend les valeurs
Si maintenant
Si on veut la loi de Y, on prend
par Anonyme » 30 Aoû 2005, 15:37
Ce n'est pas noté sur l'énoncé mais nous n'avons faits que les variables aléatoires discètes et continues.
L'énoncé est :
La loi de probabilité p(xi) d'une variable X est la suivante : puis il y a un tableau avec les valeurs de xi et pi ; xi=-1 pi=0,15 . xi=0 pi=0,25 . xi=1 pi=0,3 . xi=2 pi=0,1 . xi=3 pi=0,2.
Les 2 premières questions sont 1- construire l'histogramme de cette loi et 2- calculer l'espérance mathématique de X et de X²
L'énoncé est :
La loi de probabilité p(xi) d'une variable X est la suivante : puis il y a un tableau avec les valeurs de xi et pi ; xi=-1 pi=0,15 . xi=0 pi=0,25 . xi=1 pi=0,3 . xi=2 pi=0,1 . xi=3 pi=0,2.
Les 2 premières questions sont 1- construire l'histogramme de cette loi et 2- calculer l'espérance mathématique de X et de X²
par Galt » 30 Aoû 2005, 17:15
Dans ce cas, il n'y a pas de problème, sauf que les valeurs -1 et 1 de X vont donner la même valeur 1 pour Y.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :