Probabilités

[Johnny]

Je suis dans le néant face à ces deux problèmes.
Je poste ici en espérant que quelqu'un puisse me guider.

1) Soit X une variable aléatoire suivant une loi exponentielle de paramètre ;) > 0. On pose Y = [X], où [x] désigne la partie entière de x ;) R.

a) Calculer la loi suivie par Y
b) Soit Z = X - Y. Calculer l'espérance et la variance de Z.


2) Soient X et Y deux variables aléatoires à valeurs dans N telle que
P(X = k | Y = n) = 1/(n+1) pour 0 ;) k ;) n et 0 sinon

a) Trouver la loi deux couples (X,Y) en fonction de la loi de Y
b) Montrer que P(X ;) Y) = 1
C) Soit a ;) ]0,1[. On suppose que P(Y = n) = (1 - a)²(n+1)a^n. Trouver les lois de X puis de Y - X.

[Touriste]

Bonjour,

Je suis dans le néant face à ces deux problèmes.
Je poste ici en espérant que quelqu'un puisse me guider.

Je ne peux laisser quelqu'un dans le néant devant un exo de probas ! Voici donc quelques questions qui vont servir à te débloquer...

1) Soit X une variable aléatoire suivant une loi exponentielle de paramètre > 0. On pose Y = [X], où [x] désigne la partie entière de x R.
a) Calculer la loi suivie par Y

Quelles sont les valeurs prises par Y ?
(Pour la question b, tu as besoin du a donc je laisse provisoirement tomber)

2) Soient X et Y deux variables aléatoires à valeurs dans N telle que
P(X = k | Y = n) = 1/(n+1) pour 0 k n et 0 sinon
a) Trouver la loi du couple (X,Y) en fonction de la loi de Y

X et Y sont à valeurs dans N donc trouver la loi de (X,Y), c'est déterminer les valeurs P[X=k,Y=n] pour k et n dans N. Ne connais-tu pas une fomule que lie la proba de ton énoncé et celle-là ?

J'attends tes réponses et on poursuit ces exos !

[Johnny]

Quelles sont les valeurs prises par Y ?
(Pour la question b, tu as besoin du a donc je laisse provisoirement tomber)

J'ai me suis relu et et je n'ai pas fait d'erreurs dans la retranscription du problème. On ne spécifie pas de valeurs pour Y. Est-il possible de faire quelque chose avec un intervalle indéfini?

X et Y sont à valeurs dans N donc trouver la loi de (X,Y), c'est déterminer les valeurs P[X=k,Y=n] pour k et n dans N. Ne connais-tu pas une fomule que lie la proba de ton énoncé et celle-là ?

hmm.. serait-ce avec la convolution? Cependant, même avec ça je ne saurais comment m'y prendre..

J'attends tes réponses et on poursuit ces exos !

Merci encore!

[Touriste]

J'ai me suis relu et et je n'ai pas fait d'erreurs dans la retranscription du problème. On ne spécifie pas de valeurs pour Y.

Je n'ai pas dit que l'énoncé était incomplet ! Y est défini comme étant la partie entière de X où X est une variable de loi exponentielle (donc à valeurs dans ). Quelles peuvent donc être les valeurs prises par Y ? Si tu préfères, je peux reformuler ma question de la façon suivante : quel est l'espace d'arrivée de la fonction définie sur qui à x associe sa partie entière ?
C'est toujours la première question à se poser quand on cherche la loi d'une variable aléatoire.

hmm.. serait-ce avec la convolution? Cependant, même avec ça je ne saurais comment m'y prendre..

Non, c'est beaucoup trop compliqué la convolution ! Et puis, généralement, en proba la convolution ne sert que pour trouver la densité d'une somme de v.a. indépendantes ayant des densités.
Ne connais-tu pas une formule du style : ?

[Johnny]

Je n'ai pas dit que l'énoncé était incomplet ! Y est défini comme étant la partie entière de X où X est une variable de loi exponentielle (donc à valeurs dans ). Quelles peuvent donc être les valeurs prises par Y ? Si tu préfères, je peux reformuler ma question de la façon suivante : quel est l'espace d'arrivée de la fonction définie sur qui à x associe sa partie entière ?
C'est toujours la première question à se poser quand on cherche la loi d'une variable aléatoire.

Puisque Y = [X], les valeurs prises par Y devraient être l'ensemble N dans [0,+;)[ ?

Non, c'est beaucoup trop compliqué la convolution ! Et puis, généralement, en proba la convolution ne sert que pour trouver la densité d'une somme de v.a. indépendantes ayant des densités.
Ne connais-tu pas une formule du style : ?

Est-ce que ce serait quelque chose comme:

P(X = k | Y = n) = P(X = k, Y = n)/P(Y = n) = 1/(n+1) ?

[Touriste]

Puisque Y = [X], les valeurs prises par Y devraient être l'ensemble N dans [0,+;)[ ?

Exact. De ce fait, trouver la loi de Y, c'est trouver les valeurs des pour tout . Mais ssi . Et comme tu connais la loi de X, tu dois trouver celle de Y.
Ecris les détails et dis-moi si ça coince.

Est-ce que ce serait quelque chose comme:

P(X = k | Y = n) = P(X = k, Y = n)/P(Y = n) = 1/(n+1) ?

Oui. Donc (c'est cette valeur qu'on te demande).

[kaya]

sans paraître trop naïf, juste une question, c'est quoi déjà loi exponentielle
je crois que je pourrais faira analogie avec un autre exo de même genre

[Touriste]

suit la loi exponentielle de paramètre si admet pour densité .

[kaya]

Pour la 1)
on a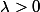 , donc on a une courbe de la densité de X décroissante vers 0 et prend la valeur initiale et on a Y=[X]. pour mieux comprendre fixons par exemple (ce n'est qu'une exemple hein...) Donc Y={0,1,2,3,4,5}.
Y=5 si X est dans [5.5,5]
Y=4 si est dans l'intervale [4,5[
Y=3 -------------------- [3,4[ et ainsi de suite... n'est-ce pas?

et maintenant on cherche x pour X=5, X=4 et ...
d'où la loi de Y selon la valeur de x. on a plus qu' à généraliser sur où Y={0,...,[-1],[]}
je crois c'est le point essentiel du problème, le reste doit marcher avec

[Touriste]

Erreur : une variable de loi exponentielle n'est pas majorée ! Y peut prendre TOUTES les valeurs dans N.

[Johnny]

Pour la question 1, je crois être en mesure d'y arriver.

Toutefois, je suis confus face à la question 2 puisque l'on ne connaît pas la P(Y = n)...

[nyafai]

ben justement ! on te demande le résultat en fonction de la loi de Y et P(Y=n) est la loi de Y