Bonjour,
Je ne comprends pas la justification de Sylvie Méléard dans son livre "Aléatoire" sur l'introduction à la théorie des probabilités, concernant la convergence presque sûre d'une suite de variables aléatoires.
Definition de Sylvie Méléard de la convergence nulle : "la suite (Xn) converge presque sûrement vers X, s'il existe un ensemble N appartient à A de probabilité nulle tel que Xn(w) tend vers X (w) quand n tend vers l'infini pour tout w n'apppartenant pas à N."
A est une tribu sur Omega, espace d'états.
Exemple donné par Sylvie Méléard: "soit U une variable aléatoire uniforme sur [0 ; 1]. Posons Zn=1 pour U inférieur ou égal à 1, 0 sinon. Alors prob (Zn=1) = 1/n et Prob (Zn=0) = 1-1/n".
Alors: "la suite Zn converge presque sûrement vers 0".
Explication de Sylvie Méléard: "En effet si w est fixé alors dés que U(w) > 0 (ce qui est vrai avec probalilité 1) il existe n0 tel que U(w) > 1/n0, et donc tel que Zn(w) = 0, pour tout n plus grand ou égal à n0".
Je comprends bien la justification que Xn(w) tend vers 0, 0 étant alors vu comme une variable aléatoire de valeur fixe. Mais où est l'ensemble N de probabilité nulle de la définition ?
Il faut bien que cet ensemble existe pour que la définition soit remplie, non ?
Merci pour vos lumières !
Probabilités : convergence presque sûre
12 messages
- Page 1 sur 1
Re: Probabilités : convergence presque sûre
Bonsoir,
Tu as fait une coquille : il faut lire "Posons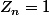 pour
pour  inférieur ou égal à
inférieur ou égal à 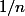 ".
".
Ensuite, Sylvie Méléard t'a donné l'ensemble : c'est le complémentaire de l'ensemble des
: c'est le complémentaire de l'ensemble des 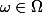 tels que
tels que >0) , c.-à-d. l'ensemble des
, c.-à-d. l'ensemble des  tels que
tels que =0) .
.
Tu as fait une coquille : il faut lire "Posons
Ensuite, Sylvie Méléard t'a donné l'ensemble
Re: Probabilités : convergence presque sûre
Merci. Oui, pardon pour la coquille.
Merci pour l'ensemble N. Je comprends qu'il est de probabilité nulle pour n infini.
A-t-on a le "droit" de donner un ensemble "négligeable" (N ici) pour un rang n non réel (car N est de probabilité nulle seulement pour n infini, or n infini n'est jamais atteint, donc la probabilité nulle n'est jamais atteinte non plus) ?
Un grand merci !
Merci pour l'ensemble N. Je comprends qu'il est de probabilité nulle pour n infini.
A-t-on a le "droit" de donner un ensemble "négligeable" (N ici) pour un rang n non réel (car N est de probabilité nulle seulement pour n infini, or n infini n'est jamais atteint, donc la probabilité nulle n'est jamais atteinte non plus) ?
Un grand merci !
Re: Probabilités : convergence presque sûre
Merci pour l'ensemble N. Je comprends qu'il est de probabilité nulle pour n infini.
Qu'est-ce que ça veut dire ? Il n'y a aucun
Je répète :
Re: Probabilités : convergence presque sûre
Merci je comprends mieux.
Je cherche maintenant à expliciter les éléments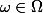 .
.
Je pense à:
 =
=
 =
=
(...)
 =
=;1/n])
Ainsi :
Z1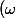) = 1 pour tout
= 1 pour tout 
Z2) = 0, Z2
= 0, Z2) = 1, Z2
= 1, Z2) = 1 ... etc
= 1 ... etc
Z3) = 0, Z3
= 0, Z3) = 0, Z3
= 0, Z3) = 1 ... etc
= 1 ... etc
Est-ce correct ?
Je cherche maintenant à expliciter les éléments
Je pense à:
(...)
Ainsi :
Z1
Z2
Z3
Est-ce correct ?
Re: Probabilités : convergence presque sûre
Non, ça ne va pas du tout. Je crois que tu ne comprends pas la notion de variable aléatoire (je reconnais que ce n'est pas tout simple).
C'est quoi, ton ? C'est quoi, sa mesure de probabilité ? C'est quoi, ta variable aléatoire
? C'est quoi, sa mesure de probabilité ? C'est quoi, ta variable aléatoire  qui a une loi uniforme sur
qui a une loi uniforme sur 
C'est quoi, ton
Re: Probabilités : convergence presque sûre
Bonjour,
Merci de continuer sur ce sujet. J'ai revu le texte de Sylvie Méléard pour répondre précisément à chacune des trois questions :
C'est quoi mon ?
?
C'est l'espace de tous les résultats possibles de mon expérience aléatoire "tirage d'un nombre compris entre 0 et 1". C'est donc l'intervalle [0 ; 1].
Un résultat possible de cette expérience est noté .
.
Je pourrais alors penser que est un nombre compris entre 0 et 1. Sauf que j'ai écarté cette possibilité pour la raison que je donne ci-après.
est un nombre compris entre 0 et 1. Sauf que j'ai écarté cette possibilité pour la raison que je donne ci-après.
C'est quoi la mesure de probabilité de
p( ) = 1.
) = 1.
Une [mesure de] probabilité est une application d'un ensemble de parties de (parties composées de certains résultats de l'expérience, on appelle ces parties "événements") dont on peut mesurer la chance de réalisation, vers [0 ; 1].
(parties composées de certains résultats de l'expérience, on appelle ces parties "événements") dont on peut mesurer la chance de réalisation, vers [0 ; 1].
Donc pour moi, si est un réel, alors P(
est un réel, alors P( ) = 0. Si
) = 0. Si  est un intervalle, alors P(
est un intervalle, alors P( ) est non nul. Voilà pourquoi j'ai proposé des intervalles.
) est non nul. Voilà pourquoi j'ai proposé des intervalles.
C'est quoi ma variable aléatoire U
C'est une fonction de la variable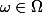 .
.
La variable aléatoire U est une application de l'espace probabilisable ( , A) [ou A est la tribu des événements de
, A) [ou A est la tribu des événements de  ) dans un ensemble F :
) dans un ensemble F :
 \in) F
F
Ici F est l'intervalle [0 ; 1]
Merci de continuer sur ce sujet. J'ai revu le texte de Sylvie Méléard pour répondre précisément à chacune des trois questions :
C'est quoi mon
C'est l'espace de tous les résultats possibles de mon expérience aléatoire "tirage d'un nombre compris entre 0 et 1". C'est donc l'intervalle [0 ; 1].
Un résultat possible de cette expérience est noté
Je pourrais alors penser que
C'est quoi la mesure de probabilité de
p(
Une [mesure de] probabilité est une application d'un ensemble de parties de
Donc pour moi, si
C'est quoi ma variable aléatoire U
C'est une fonction de la variable
La variable aléatoire U est une application de l'espace probabilisable (
Ici F est l'intervalle [0 ; 1]
Re: Probabilités : convergence presque sûre
Il reste tout de même pas mal de confusion dans ce que tu écris. Essayons d'y voir plus clair.
Tu prends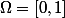 , c'est un choix raisonnable. Quand je demandais la mesure de probabilité, ce n'était bien sûr pas seulement le fait que la mesure de l'espace complet est 1. Bon, on prend la mesure de Lebesgue, celle pour laquelle la mesure de proba de l'intervalle
, c'est un choix raisonnable. Quand je demandais la mesure de probabilité, ce n'était bien sûr pas seulement le fait que la mesure de l'espace complet est 1. Bon, on prend la mesure de Lebesgue, celle pour laquelle la mesure de proba de l'intervalle  contenu dans
contenu dans  est
est 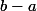 .
.
Un élément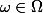 est un nombre réel dans
est un nombre réel dans  , ce n'est pas un intervalle !
, ce n'est pas un intervalle !
La variable aléatoire est tout simplement l'identité :
est tout simplement l'identité : =\omega) (je rappelle que
(je rappelle que  est un réel dans
est un réel dans  ).
).
Ce qui est important, c'est la loi de . C'est bien la loi uniforme sur
. C'est bien la loi uniforme sur  .
.
Tu prends
Un élément
La variable aléatoire
Ce qui est important, c'est la loi de
Re: Probabilités : convergence presque sûre
Bonjour,
Oui. J'ai continué à réfléchir après avoir écrit.
En fait, je commets l'erreur de penser qu'un candidat pour doit avoir une probabilité non nulle. Ce qui m'amène à penser à un intervalle de [0 ; 1] pour
doit avoir une probabilité non nulle. Ce qui m'amène à penser à un intervalle de [0 ; 1] pour  .
.
Or rien n'interdit que cette probabilité soit nulle pour .
.
Car pour identifier on ne s'intéresse pas à la probabilité d'obtenir
on ne s'intéresse pas à la probabilité d'obtenir ) : seule entre en jeu la valeur prise par
: seule entre en jeu la valeur prise par ) .
.
La probabilité d'obtenir) est d'ailleurs nulle aussi.
est d'ailleurs nulle aussi.
J'ai donc qui est en réalité un nombre réel compris entre 0 et 1 et est de probabilité nulle.
qui est en réalité un nombre réel compris entre 0 et 1 et est de probabilité nulle.
Oui. Je comprends que) dans mon cas est égal à
dans mon cas est égal à  .
.
Merci beaucoup pour votre aide.
Oui. J'ai continué à réfléchir après avoir écrit.
En fait, je commets l'erreur de penser qu'un candidat pour
Or rien n'interdit que cette probabilité soit nulle pour
Car pour identifier
La probabilité d'obtenir
J'ai donc
Oui. Je comprends que
Merci beaucoup pour votre aide.
Re: Probabilités : convergence presque sûre
Pardon, par ) je veux dire
je veux dire ) mais je ne peux plus modifier le message précédent.
mais je ne peux plus modifier le message précédent.
Re: Probabilités : convergence presque sûre
Ce n'est visiblement pas encore très clair.
La variable aléatoire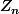 , toujours dans la formalisation où
, toujours dans la formalisation où  muni de la mesure de probabilité de Lebesgue et
muni de la mesure de probabilité de Lebesgue et  , est la fonction
, est la fonction  définie par
définie par =1) si
si  et
et =0) si
si  . On a donc
. On a donc =1/n) et
et =1-1/n) . La probabilité que
. La probabilité que 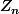 prenne la valeur
prenne la valeur  n'est donc jamais nulle. Ce qui se passe, c'est que pour tout
n'est donc jamais nulle. Ce qui se passe, c'est que pour tout  , la suite
, la suite )) converge vers 0 : elle vaut en fait 0 à partir d'un certain rang. Comme la mesure de proba de
converge vers 0 : elle vaut en fait 0 à partir d'un certain rang. Comme la mesure de proba de  est nulle, cela veut dire que la suite de variables aléatoires
est nulle, cela veut dire que la suite de variables aléatoires ) converge presque sûrement vers 0.
converge presque sûrement vers 0.
La variable aléatoire
Re: Probabilités : convergence presque sûre
Oui, pardon pour la coquille, la probabilité nulle est celle de U( ), et non pas celle de
), et non pas celle de ) , puisque U(
, puisque U( ) =
) =  . Pour le reste, vos explications sont claires.
. Pour le reste, vos explications sont claires.
Merci beaucoup.
Merci beaucoup.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
