Convergence presque sûre loi uniforme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathpath
- Messages: 1
- Enregistré le: 07 Avr 2021, 11:35
-
 par mathpath » 07 Avr 2021, 11:46
par mathpath » 07 Avr 2021, 11:46
Soit X1, X2, ... des variables aléatoires indépendantes identiquement distribuées uniformément sur (0, 1), et soit
f ∶ [0, 1] → R continue et bornée. je dois montrer que :
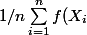 \rightarrow \int_{0}^{1} f(u) du)
. La convergence ici est presque sure.
Merci d'avance
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Avr 2021, 16:50
par Sylviel » 07 Avr 2021, 16:50
C'est pratiquement une application directe de la loi forte des grands nombres.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités