Probabilité

[camille75]

bonjour je dois calculer la proba d'obtenir exactement 2 trèfle et 3 as en tirant une poignée de 6 cartes au hasard ds un jeu de 32

pouvez vous me dire si ce que je trouve est bon ?

je pose A l'événement "obtenir 2 trèfles et 3 as

card A =(2 parmis 8)*(3parmis3).*(1 parmis 21)+(1parmis7)*(2 parmis 3)*(1parmis1)*(2parmis21)

card(oméga)=(6parmis32)

donc P(A)=card(A)/card(omega)

est ce exact?

merci :)

[Finrod]

Pourrais-tu expliquer ton raisonnement ?

No, parce que la tu as tiré 12 cartes.

Je pense aussi que tu n'a pas compris le sens du .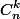

Tu tires 6 cartes et tu t'intéresses donc a des combinaisons de 6 cartes : le n en bas vaudra donc toujours 6... par exemple est le nombre de façon de placer deux trèfles parmi 6 cartes sans se soucier de la valeur des autres.


Enfin, Il y a un piège avec l'as de treffle ( mais ça tu l'as vu) qui est une carte à part.

[camille75]

je vois deux cas possibles:

1er cas (2parmi8)(3parmi3)(1parmi 21): je tire 2 trèfles parmi les 8 puis 3 as parmi 3 j'ai enlevé l'as de trèfle puis 1 carte parmi 21 j'ai enlevé tout les trèfles + les 3 as

2ème cas: (1parmi7)(1 parmi1)(1parmi3)(2 parmi 31) je tire 1 trèfle parmi 7 j'ai retiré l'as puis je tire l'as de trèfle donc 1 parmi 1 puis 1 as parmis 3 j'ai enlevé l'as de trèfle et enfin 2 cartes parmi 21 j'ai enlevé les trèfle et les 3 as

et pour prendre en compte ces 2 cas possibles j'ai additionné le tout

[Finrod]

1 parmi 21 ne signifie pas "je tire une carte parmi 21". Il compte le nombre positionnement différent de ta carte dans un tirage de 21 cartes.

De même 2 parmi 31 compte le nombre de positions de deux cartes identiques (deux trèfles par ex) dans un tirage de 31 cartes.

Ici ton tirage fait 6 cartes. Donc tu ne peux avoir que des x parmi 6, on est d'accord ?


Bon après, il ne faut pas utiliser de (k parmi n) de toute façon car ils servent au cas de comptage lorsque l'ordre est important. Ici l'ordre des cartes ne nous intéresse pas !

C'est donc des proba de base avec tirage sans remise.

[camille75]

je vois pas du tout comment on fait alors :help:

[fatal_error]

Bon après, il ne faut pas utiliser de (k parmi n) de toute façon car ils servent au cas de comptage lorsque l'ordre est important. Ici l'ordre des cartes ne nous intéresse pas !

Euh, faut faire gaffe au contexte, parce que la comme ca (sans lire ce qui précède), c'est sonne pas super. Arrangement pour l'ordre, combinaison sans ordre.

Ici ton tirage fait 6 cartes. Donc tu ne peux avoir que des x parmi 6, on est d'accord ?

Je suis pas d'accord non plus.
Le nombre de mains totale, c'est .

Maintenant, on cherche le nombre de mains solutions.
Premier cas : on pioche l'as de trefle.

Où : le 1 représente l'as de trefle
Le deuxieme facteur représente une carte a trefle sur les 12 restantes a trefle
Le troisieme facteur représente deux as parmi les trois restants
Et le dernier facteur représente 2 cartes a piocher pour compléter la main de 6, ou n désigne le nombre de cartes restantes (qui ne doivent pas etre un as ni un trefle).

Le deuxieme cas : on ne pioche pas l'as de trefle.

Apres, ben on somme.

[Finrod]

Non après réflexion, comme c'est sans remise, l'ordre compte un peu.

excuse moi.

et il faut donc les tirer une par une en séparant les tirages avec l'as de trèfle et ceux sans, comme tu essais de la faire depuis le début.
Il faut aussi séparer je pense en fonction de l'ordre de tirage des as et des trèfles et de la carte ni as ni trèfle qui complète.
Ce qui fait (2 parmi 5)*(2parmi 3) possibilités soit 30 possibilités qui ont toutes une proba différentes. (uniquement pour le cas sans l'as de trèfle).

c'est rude en fait. C'est plus dur que la plupart des exos de prépa que j'ai donné ou vu.

@Fatal_error -> Oui,un coup de fatigue, je m'en suis rendu compte

Je vais aller réviser mes dénombrements moi. Le raisonnement que je viens de faire là n'est pas techniquement faux mais il est sacrément barbare et inutile.

-> Suis la méthode de fatal error.

[camille75]

au final j'ai bon ou j'ai faux ???

[Finrod]

Lit bien ce qu'a écrit fatal error.

Ton raisonnement allait dans la bonne direction, mais chacun des chiffres du haut des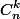 correspond à une carte tirée, et c'est en fonction de cela que Fatal choisis les bon .

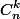Si tu regardes ton raisonnement en détails, tu verras que tu as tiré 12 cartes au lieu de 6, par exemple.