Bonjour, j'ai une question de devoir que je n'arrives pas a faire sur les loi de probabilité :
Le jeu de carte est formé de 100 cartes, numérotees de 1 a 100.
Le jeu est bien mélangé. On fixe un entier n quelconque, avec n ≤ 100.
1. Elle tire n cartes du jeu, sans remise. On note X la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées.
(a) Trouver la loi de X.
(b) Montrer que l'expérience de X vérifie E[X] = 101n /n+1
2.La personne tire n cartes (avec n ≤ 100) du jeu, avec remise cette fois-ci. On note Y la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tir ́ees.
(a) Trouver la fonction de répartition de Y .
(b) En déduire la fonction de masse de Y .
Probabilité 1
6 messages
- Page 1 sur 1
Re: Probabilité 1
Tâtonnons.
Quelle est la probabilité que le plus grand n° soit 0 ? bof.
Regardons plutôt l'autre extrémité, quelle est la proba que le plus grand n° soit 100 ?
Puis quelle est la proba que le plus grand n° soit 99 ? puis 98 ?
Et peut-être qu'on va voir se dessiner une formule ?
Au moins, on aura essayé, et on pourra expliquer au prof ce qu'on a fait.
Quelle est la probabilité que le plus grand n° soit 0 ? bof.
Regardons plutôt l'autre extrémité, quelle est la proba que le plus grand n° soit 100 ?
Puis quelle est la proba que le plus grand n° soit 99 ? puis 98 ?
Et peut-être qu'on va voir se dessiner une formule ?
Au moins, on aura essayé, et on pourra expliquer au prof ce qu'on a fait.
Re: Probabilité 1
Bonjour,
Pour la question 1:
Comme te l'a conseillé lycéen95, il faut y aller par étapes pour dégager une formule.
Considère déjà les cas simples où la personne tire sans remise:
Grâce à ces résultats, tente de faire la même chose pour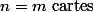
Tu pourras alors en déduire une formule générale pour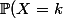)
Pour la question 1:
Comme te l'a conseillé lycéen95, il faut y aller par étapes pour dégager une formule.
Considère déjà les cas simples où la personne tire sans remise:
Grâce à ces résultats, tente de faire la même chose pour
Tu pourras alors en déduire une formule générale pour
Re: Probabilité 1
1.a.
Soit : la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées
: la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées
Soit le nombre de cartes tirées
le nombre de cartes tirées
On en déduit alors la loi de :
:
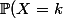 = \begin{cases} \frac{\dbinom{k-1}{n-1}}{\dbinom{100}{n}}, & \text{si }k \geq n \\ 0 & \text{sinon} \end{cases})
Soit
Soit
On en déduit alors la loi de
Re: Probabilité 1
1.b.
De ce qui précède, on établit un résultat intermédiaire:
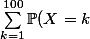 = \sum_{k=n}^{100} \mathbb{P}(X=k) =\sum_{k=n}^{100}\frac{\dbinom{k-1}{n-1}}{\dbinom{100}{n}} = 1)
Ainsi
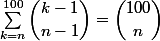
On en déduit:

Calculons l'espérance de
=\sum_{k=1}^{100} k \times \mathbb{P}(X=k)=\sum_{k=n}^{100} k \times \mathbb{P}(X=k) =\sum_{k=n}^{100} k \frac{\dbinom{k-1}{n-1}}{\dbinom{100}{n}}=\frac{\sum_{k=n}^{100} k \dbinom{k-1}{n-1}}{\dbinom{100}{n}})
Or, par la formule de factorisation des coefficients binomiaux, on a

Ainsi
=\frac{\sum_{k=n}^{100} n \dbinom{k}{n}}{\dbinom{100}{n}}=n \times\frac{\sum_{k=n}^{100} \dbinom{k}{n}}{\dbinom{100}{n}} \overset{(1)}{=} n \times \frac{\dbinom{101}{n+1}}{\dbinom{100}{n}})
Soit
=n \times \dfrac{ 101!\times n! \times(100-n)!}{(n+1)! \times (100-n)! \times 100!} =\dfrac{ 101 n }{n+1})
De ce qui précède, on établit un résultat intermédiaire:
Ainsi
On en déduit:
Calculons l'espérance de
Or, par la formule de factorisation des coefficients binomiaux, on a
Ainsi
Soit
Re: Probabilité 1
Pour en finir avec le sujet:
2. a.
Soit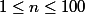 le nombre de cartes tirées.
le nombre de cartes tirées.
Soit : la variable aléatoire représentant le numéro obtenu au tirage n°
: la variable aléatoire représentant le numéro obtenu au tirage n° 
Soit : la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées.
: la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées.
On a
 = \dfrac{k}{100} \textrm{ et }Y = \underset{ 1 \leq i \leq n}{\max} (X_i))
Ainsi, la fonction de répartition de est donnée par:
est donnée par:
=\mathbb{P}(Y \leq k) =\mathbb{P}(\underset{ 1 \leq i \leq n}{\max} (X_i) \leq k) = \mathbb{P}(X_1 \leq k, X_2 \leq k, ..., X_n \leq k))
= \prod_{i=1}^n \mathbb{P}(X_i \leq k)= \prod_{i=1}^n \dfrac{k}{100} = \dfrac{k^n}{100^n})
2. b.
On en déduit alors la loi de
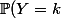 = \mathbb{P}(Y \leq k) - \mathbb{P}(Y \leq k-1) =\dfrac{k^n-(k-1)^n}{100^n} ~,~ 1 \leq k \leq 100)
2. a.
Soit
Soit
Soit
On a
Ainsi, la fonction de répartition de
2. b.
On en déduit alors la loi de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
