Bonjour,
J'ai du mal à faire mon exo . Voilà l'énoncé :" Une urne contient 6 boules dont 4 blanches et 2 noires. On extrait une boule de l'urne, on note sa couleur, puis on la remet dans l'urne. On effectue ensuite des tirages sans remise jusqu'à l'obtention d'une boule de la même couleur que précédement. Déterminer la loi de probabilité du nombre X de tirage après remise de la boule tirée initialement.
J'ai fait un arbre. Mai j'ai du mal avec la suite.
Pourrier vous m'aider en me donnant quelques piste de réponse?
Merci d'avance.
Bonne journée.
Probabilité
8 messages
- Page 1 sur 1
Bonjour, :happy3:
En fait, lexpérience énoncé dans ton problème ressemble fort à une distribution qui suit une loi géométrique, à quelques petites différences près, qui est que dans le cas de la loi géométrique, la succession des tirages donne des issus indépendantes les uns des autres, ce qui n'est pas le cas de ton tirage ( sans remise, malheureusement ).
Donc, essaye de voir de ce coté là, vérifie ce qu'est d'abord une loi géométrique, ensuite, fais un effort pour décrire la loi que tu recherches en s'inspirant de la loi géométrique.
Cordialement. :happy3:
En fait, lexpérience énoncé dans ton problème ressemble fort à une distribution qui suit une loi géométrique, à quelques petites différences près, qui est que dans le cas de la loi géométrique, la succession des tirages donne des issus indépendantes les uns des autres, ce qui n'est pas le cas de ton tirage ( sans remise, malheureusement ).
Donc, essaye de voir de ce coté là, vérifie ce qu'est d'abord une loi géométrique, ensuite, fais un effort pour décrire la loi que tu recherches en s'inspirant de la loi géométrique.
Cordialement. :happy3:
Bonjour,
Si tu as déjà réalisé l'arbre complet (avec à la racine le choix de couleur de la boule initiale, puis les tirages jusqu'à retrouver la même couleur), l'exercice est fini.
Pour chaque feuille de ton arbre tu connais sa probabilité d'être réalisée (produit des probas à chaque noeud jusqu'à la feuille), et chaque feuille est liée à un nombre d'essais pour retrouver la couleur.
Tu n'as donc plus qu'à regrouper les feuilles par nombre d'essais et sommer leur probabilité pour obtenir la loi : pour X = 1, je regarde toutes les feuilles de l'arbre qui correspondent à une situation ou on est retombé sur la même couleur du premier coup : il y en a deux : boule initiale Noire puis premier tirage Noir, et Boule initial blanche puis 1er tirage blanc. On somme leurs probabilités et ça nous donne la probabilité de X=1. Même chose pour X=2,3...
Damien
Si tu as déjà réalisé l'arbre complet (avec à la racine le choix de couleur de la boule initiale, puis les tirages jusqu'à retrouver la même couleur), l'exercice est fini.
Pour chaque feuille de ton arbre tu connais sa probabilité d'être réalisée (produit des probas à chaque noeud jusqu'à la feuille), et chaque feuille est liée à un nombre d'essais pour retrouver la couleur.
Tu n'as donc plus qu'à regrouper les feuilles par nombre d'essais et sommer leur probabilité pour obtenir la loi : pour X = 1, je regarde toutes les feuilles de l'arbre qui correspondent à une situation ou on est retombé sur la même couleur du premier coup : il y en a deux : boule initiale Noire puis premier tirage Noir, et Boule initial blanche puis 1er tirage blanc. On somme leurs probabilités et ça nous donne la probabilité de X=1. Même chose pour X=2,3...
Damien
Re-bonjour :
Puisque le tirage se fait sans remise, alors là, on a affaire à des probabilités conditionnelles ( vaut mieux construire un arbre pondéré à une seule branche pour comprendre comment cela fonctionne ). Le tirage suivant est toujours influencé par le tirage précédent, car le tirage s'effectue sans remise.
Donc, contrairement à la loi géométrique qui donne une succession de tirage indépendantes, ( donc pas de probabilités conditionnelles ) où on obtient comme loi : = pp \dots pq = p^{k-1} q) , ici les successions de tirages se font sans remise ( donc, il y'a probabilités conditionelles ), où la loi est définie par :
, ici les successions de tirages se font sans remise ( donc, il y'a probabilités conditionelles ), où la loi est définie par : 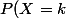 = p_1 p_2 \dots p_{k-1} q) avec :
avec : 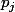 à définir combinatoirement où
à définir combinatoirement où  . J'ai du mal à trouver la formule pour le moment. :hum:
. J'ai du mal à trouver la formule pour le moment. :hum:
On peut en déduire la formule par récurrence : On cherche ensuite
ensuite 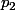 ensuite
ensuite 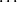 ensuite
ensuite ) avec
avec  à déterminer.
à déterminer.
Puisque le tirage se fait sans remise, alors là, on a affaire à des probabilités conditionnelles ( vaut mieux construire un arbre pondéré à une seule branche pour comprendre comment cela fonctionne ). Le tirage suivant est toujours influencé par le tirage précédent, car le tirage s'effectue sans remise.
Donc, contrairement à la loi géométrique qui donne une succession de tirage indépendantes, ( donc pas de probabilités conditionnelles ) où on obtient comme loi :
On peut en déduire la formule par récurrence : On cherche
Salut,
S'il y a noires et
noires et  blanches (je deteste les valeurs numériques...) et qu'on cherche la proba.
blanches (je deteste les valeurs numériques...) et qu'on cherche la proba. 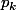 qu'il faille attendre
qu'il faille attendre  tirages pour tirer la première blanche (avec
tirages pour tirer la première blanche (avec  ), on a :
), on a :
 (proba de tirer directement une blanche)
(proba de tirer directement une blanche)
 (tirer une noire puis une blanche sur les
(tirer une noire puis une blanche sur les  restantes)
restantes)
 (noire puis noire puis blanche)
(noire puis noire puis blanche)

...
(n-2)...(n-(k-2))\,b}{(n+b)(n+b-1)(n+b-2)...(n+b-(k-1))}\,<br />=\,\frac{n!(n+b-k)!\,b}{(n+1-k)!(n+b)!}\,<br />=\,\frac{(n+b-k)!}{(n+1-k)!(b-1)!}\times\frac{n!b!}{(n+b)!}\,<br />=\,{n+b-k \choose b-1}\,/\,{n+b \choose b})
Idem pour les noires avec (pour
(pour  )
)
Et la proba recherché est donc
Bon, O.K., j'admet que dans un exo avec et
et 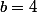 , c'est p'têt pas ça qui est attendu comme réponse... :doh:
, c'est p'têt pas ça qui est attendu comme réponse... :doh:
S'il y a
...
Idem pour les noires avec
Et la proba recherché est donc
Bon, O.K., j'admet que dans un exo avec
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Application Numérique :  ,
, 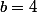 donc
donc 
En regardant la 4em colonne du triangle de pascal, les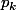 valent
valent  ,
, 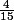 ,
,  .
.
En regardant la 2em colonne du triangle de pascal, les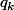 valent
valent  ,
, 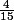 ,
,  ,
,  ,
,  .
.
Donc les\) valent
valent  ,
,  ,
,  ,
,  ,
,  .
.
En regardant la 4em colonne du triangle de pascal, les
En regardant la 2em colonne du triangle de pascal, les
Donc les
donc c'est bon !!!dream2passion a écrit:J'ai fait sa :
P(X=1)= P(B;B)+P(N;N)=2/3*2/3+1/3+1/3=5/9
P(X=2)=P(B;N;B)+P(N;B;N)=2/3*1/3*4/5+1/3*2/3*2/5=4/15
P(X=3)=P(B;N;N;B)+P(N;B;B;N)=2/3*1/3*1/5*1+1/3*2/3*3/5*1/2=1/9
P(X=4)=P(N;B;B;B;N)=1/3*2/3*3/5*1/2*2/3=2/45
P(X=5)=P(N;B;B;B;B;N)=1/3*2/3*3/5*2/4*1/3*1=1/45
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
