Primitive d'une fonction irrationnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Studenthec
- Membre Naturel
- Messages: 16
- Enregistré le: 18 Oct 2006, 17:23
-
 par Studenthec » 30 Déc 2006, 14:04
par Studenthec » 30 Déc 2006, 14:04
Bonjour à tous,
Je suis bloqué au calcul d'une primitive de type irrationnel, le problème est que je n'arrive pas à démarrer, j'ai toujours travaillé par subsitution mais là je vois pas comment faire... Voici la fonction en question :
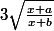
Avec a, b dans R mais a différent de b.
Si quelqu'un sait par où je devrais je commencer, ça m'aiderait beaucoup ^^.
J'ai la réponse et c'est celle-ci :
.(x+b)})
Mais j'avoue qu'elle ne m'aide pas à démarrer ^^'.
Merci beaucoup.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2006, 14:15
par Nightmare » 30 Déc 2006, 14:15
Bonjour :happy3:
Pose
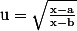
Tu n'auras plus qu'une fraction rationnelle à intégrer
:happy3:
-
Studenthec
- Membre Naturel
- Messages: 16
- Enregistré le: 18 Oct 2006, 17:23
-
 par Studenthec » 30 Déc 2006, 14:25
par Studenthec » 30 Déc 2006, 14:25
J'ai essayé mais mon du devient
^{2}}.dx)
Je vois pas trop comment remplacer là-dedans (j'aime pas les racines ^^')
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2006, 14:33
par Nightmare » 30 Déc 2006, 14:33

Par conséquent :
u}{(u^{2}-1)^{2}}du)
u}{(u^{2}-1)^{2}}du)
Un décomposition en élément simple et hop !
:happy3:
-
mathelot
 par mathelot » 30 Déc 2006, 14:37
par mathelot » 30 Déc 2006, 14:37
Nightmare a écrit:Pose
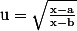
Tu n'auras plus qu'une fraction rationnelle à intégrer
tu peux calculer

en fonction de

en élevant au carré les deux termes de cette égalité et ensuite le "dx" est proportionnel au "du" via une fraction rationnelle de la variable

-
Studenthec
- Membre Naturel
- Messages: 16
- Enregistré le: 18 Oct 2006, 17:23
-
 par Studenthec » 30 Déc 2006, 14:38
par Studenthec » 30 Déc 2006, 14:38
Ca ne serait pas plutôt u =
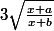
alors?
J'avais essayé quelque chose dans le genre mais je n'arrivais pas à exprimer x en fonction de u, tu y arrives comment?
Un grand merci à toi ^^
-
mathelot
 par mathelot » 30 Déc 2006, 14:42
par mathelot » 30 Déc 2006, 14:42
Studenthec a écrit:Ca ne serait pas plutôt u =
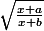
alors?
oui, c cela.
ensuite:
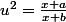
et ensuite, on exprime

en fonction de
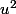
puis "dx" en fonction de

et "du"
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2006, 14:44
par Nightmare » 30 Déc 2006, 14:44
Oups oui autant pour moi, j'ai mal lu la fonction d'origine.
-
Studenthec
- Membre Naturel
- Messages: 16
- Enregistré le: 18 Oct 2006, 17:23
-
 par Studenthec » 30 Déc 2006, 14:46
par Studenthec » 30 Déc 2006, 14:46
Ah ok ^^ juste une dernière petite chose, comment vous trouvez x en fonction de u à partir de
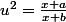
?
Après ça je devrais y arriver tout seul ^^'
Merci à tous les deux :++:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 30 Déc 2006, 14:49
par Nightmare » 30 Déc 2006, 14:49
Allons allons, c'est niveau seconde :lol3:
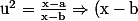u^{2}=x-a)
donc
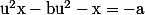
ainsi
x=bu^{2}-a)
et finalement
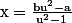
:happy3:
-
Studenthec
- Membre Naturel
- Messages: 16
- Enregistré le: 18 Oct 2006, 17:23
-
 par Studenthec » 30 Déc 2006, 14:54
par Studenthec » 30 Déc 2006, 14:54
Je sais pas pourquoi mais j'ai toujours eu du mal avec ça :p
Enfin je vais enfin pouvoir finir mes primitives irrationnelles, encore merci ^^.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
