Premier petit exercice sur le développement limité.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 30 Jan 2020, 23:24
Bonsoir
Je souhaite déterminer le développement limité de sin(3x) en 0 à l'ordre 5 avec la formule de Taylor-Young.
Pourriez vous me confirmer ou infirmer que sin(3x) <=> sin(x).3x ?
.3x= (-x +\frac{x^3}{3!} + \epsilon(x)x^5) \times (x+ \epsilon(x)x^5))
Avant de continuer pourriez-vous me dire, si j'ai bien commencé ?
Merci !!!
A bientôt
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 30 Jan 2020, 23:34
Salut !
Je ne comprends pas bien ce que tu as écrit, mais \sin(3x) \ne 3x \sin(x). C'est tout simple, tu prends le DL de la fonction sinus et tu remplaces la variable par son triple :
=x-\frac{x^3}{3!} +x^5 \epsilon(x))
où
 \to 0)
lorsque
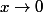
, donc :
=3x-\frac{(3x)^3}{3!} +(3x)^5 \epsilon(3x)=3x-\frac{9x^3}{2} +x^5 \epsilon'(x))
,
en posant
= 3^5 \epsilon(3x))
avec
 \to 0)
lorsque
.
-
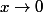
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 30 Jan 2020, 23:39
Merci de cette précision.
Je pensé avoir à faire à f o g.
-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
par Lostounet » 30 Jan 2020, 23:52
sin(x)*3x n'est pas du tout égal à sin(3x)
D'ailleurs, sin(3x) n'est pas non plus égal à 3 sin(x) ... sin n'est pas une fonction linéaire.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
par mathelot » 31 Jan 2020, 18:01
bonsoir,
à l'ordre 5, on a
=3x - \dfrac{9}{2}x^3+\dfrac{81}{40}x^5+o(x^6))
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 02 Fév 2020, 22:58
Bonsoir
mathelot comment avez vous trouvez
A bientôt
-
mathelot
par mathelot » 02 Fév 2020, 23:17
à l'ordre 5, on a
=x - \dfrac{1}{3!}x^3+\dfrac{1}{5!}x^5+o(x^6))
on change x en 3x:
=3x - \dfrac{9}{2}x^3+\dfrac{3^5}{5!}x^5+o(x^6))
or
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
par novicemaths » 02 Fév 2020, 23:33
Merci pour ce complément d'information.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
