Bonjour,
Tout d'abord, on me demande d'approximer la valeur de

à l'aide des polynomes de Taylor et d'estimer l'erreur en donnant le plus petit intervalle contenant la valeur. Le polynome doit être du second degré et l'approximation autour du point x=1.
Je n'ai aucun problème pour trouver le polynome de Taylor mais par contre je n'arrive pas à trouver l'erreur et l'intervalle dans lequel la réponse se trouve donc...
 = \frac{f^{[3]}(c)(x-1)^3}{3!})
Quand je calcule
)
, j'obtiens un polynome de la forme
^2})
mais pour pouvoir majorer cette expression de la manière la plus efficace, comment dois-je faire? Dois-je étudier ce polynome pour voir en quelles valeurs il est négatif, positif, maximal?
Ensuite, J'ai également une autre question sur un exercice où l'on me demande d'utiliser la formule de Taylor pour démontrer que:

avec
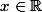
En utilisant la formule de Taylor avec un polynome de degré 1, j'obtiens :

mais comment faire le lien entre les deux inéquations étant donné que je ne connais pas la valeur de c (à part que c est situé entre 0 et x...) donc je ne connais pas le signe de

et je ne vois pas comment terminer ce problème.
Merci beaucoup pour l'aide! :lol3:
