Polynome irreductible
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
oumou
- Membre Relatif
- Messages: 137
- Enregistré le: 27 Avr 2016, 07:48
-
 par oumou » 11 Mai 2017, 07:02
par oumou » 11 Mai 2017, 07:02
bonjour, j ai des doutes sur mes reponse , est ce correct ?
soit t appartient a Z , on considere le polynome P =
 X + 1)
selon les valeurs de t appartient aZ , decomposer P en produit de facteur irreductibles de Q{x}
je dis que si t = 0 alors P =(X-1) (X+1) (
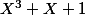
)
si t

0 alors P est irreductible dans Q(X)
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 11 Mai 2017, 08:47
par pascal16 » 11 Mai 2017, 08:47
Tu veux dire que n'importe quel valeurs de t, même entière ne permet pas de trouver une seule racine rationnelle ni d'exprimer le polynôme sous la forme un polynôme de degré 2 fois un polynôme de degré 3.
vu de loin, si on cherche des racines, on a que leur somme vaut 0 et leur produit -1, rien ne les emp^ches d'être rationnels, il faut aller plus loin
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Mai 2017, 09:55
par Doraki » 11 Mai 2017, 09:55
D'après le lemme de Gauss, si t est entier, les facteurs irréductibles sont à facteurs entiers aussi.
Et comme le coefficient dominant est +-1, leurs coefficients dominants sont aussi inversibles.
(et donc si il y a une racine elle est entière)
Pour montrer que les seuls facteurs de degré 1 possible sont (x-1) et (x+1) pour t=0, ça va encore c'est pas super dur.
Par contre pour montrer qu'il n'y a pas d'autre facteur de degré 2 c'est assez lourd j'ai l'impression.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 11 Mai 2017, 10:41
par zygomatique » 11 Mai 2017, 10:41
salut
on peut peut-être déjà voir ce que donne :
 = x^5 - tx^3 - x^2 - (t + 1)x + 1 = (x^2 + ax + b)(x^3 + cx^2 + dx + e))
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 11 Mai 2017, 11:54
par Doraki » 11 Mai 2017, 11:54
En fait, b peut être seulement 1 ou -1., ça fait pas mal avancer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités