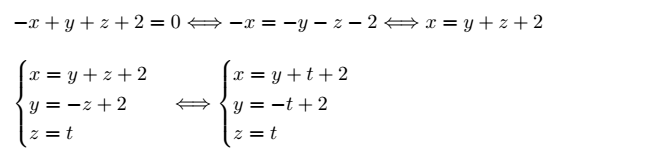Passer de l'équation cartésienne à l'équation paramétrique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 02 Jan 2021, 22:25
par novicemaths » 02 Jan 2021, 22:25
Bonsoir
Je souhaite déterminer l'équation paramétrique de la droite: -x+y+z+2=0
Voici mes calcules avec mon livre d’algèbre (pas beaucoup d’explication) :
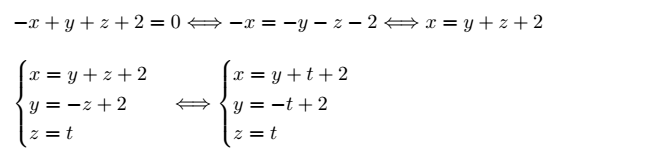
Si j'ai bien compris, il faut décomposer l'equation.
Pourriez-vous me dire quels sont mes erreurs.
A bientôt
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 02 Jan 2021, 22:53
par lyceen95 » 02 Jan 2021, 22:53
Je souhaite déterminer l'équation paramétrique de la droite: -x+y+z+2=0
Avant de commencer, est-ce que l'équation -x+y+z+2=0 est bien l'équation d'une droite ?
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 02 Jan 2021, 23:28
par novicemaths » 02 Jan 2021, 23:28
Je mérite une claque derrière la tête c'est bien l'équation d'un plan,
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 03 Jan 2021, 22:56
par novicemaths » 03 Jan 2021, 22:56
Bonsoir
J'essai de récupérer le vecteur normal et le point de l'équation -x+y+z+2=0 pour ensuite réaliser la représentation paramétrique du plan.
Je ne vois pas quel méthode utilisée.
A bientôt
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2021, 08:38
par Carpate » 04 Jan 2021, 08:38
J'essai de récupérer le vecteur normal et le point de l'équation -x+y+z+2=0 pour ensuite réaliser la représentation paramétrique du plan.
Un vecteur normal au plan est
)
Un point du plan : A(0;0;-2)
Pour établir la représentation paramétrique de ce plan il te faut 1 point du plan et 2 vecteurs directeurs du plan.
Ca peut être 2 vecteurs perpendiculaires à
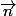
.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 04 Jan 2021, 11:27
par GaBuZoMeu » 04 Jan 2021, 11:27
Bonjour,
Un plan est de dimension 2, une représentation paramétrique du plan fera intervenir deux paramètres (deux degrés de liberté).
On peut prendre deux des coordonnées comme paramètres, par exemple y et z. Pourquoi se casser plus la tête ?
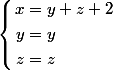
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Jan 2021, 18:33
par Carpate » 04 Jan 2021, 18:33
La solution de GaBuZoMeu est très rapide.
Une solution plus classique ou plus géométrique est de choisir 3 points du plan par exemple :
, B(1;0;-1), C(1;-1;0))
Et d'exprimer que tout vecteur
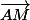
du plan s'exprime linéairement en fonction de

et

, c'est a dire qu'il existe 2 réels

et

tels que
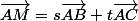
On aboutit à :
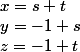
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités