Oral ccp séries ..
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par sandrine_guillerme » 01 Déc 2006, 22:59
Bonsoir tout le monde J'ai une question pas du tout évidente pour moi si vous pourrez m'aider .. serait grandement apprèciés ..
soit
f(t)=0 si t=0
f(t)=t ln(t) si
on définit donc la fonction suivante pour tout
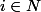
on définit
 = \frac{f(t)^i}{i!})
je souhaite calculer
\, dt)
pour
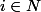
Saurez vous comment faire ..?
Merci d'avance .
P.S: c'est un problème que j'essaie de faire pour comprendre les séries et les intègrales donc si vous aurez une idée comment faire je vous prie de m'expliquer pourquoi .. Bon courage tout le monde ..
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 01 Déc 2006, 23:02
Bonsoir.
Une intégration par parties (dériver
^i)
et primitiver
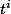
) donnerait peut-être une relation de récurrence entre
et
.
par sandrine_guillerme » 01 Déc 2006, 23:05
essais de le faire et tu verras que c'est pas aussi simple de le faire par parties .. en tout cas je tombe sur des calculs très tordus .. :mur: et si t'arrive tu peux le montrer stp?
-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
par nuage » 01 Déc 2006, 23:41
Salut,
En faisant une intégration par parties :
^n } = \left[\frac{1}{n+1} t^{n+1} (\ln t)^n \right]_0^1- \frac{n}{n+1} \int_0^1 {t^n (\ln t)^{n-1} }= - \frac{n}{n+1} \int_0^1 {t^n (\ln t)^{n-1} })
puis en recommençant :
^{n-1} } = \left[\frac{1}{n+1} t^{n+1} (\ln t)^{n-1} \right]_0^1- \frac{n-2}{n+1} \int_0^1 {t^n (\ln t)^{n-2} })
et ainsi de suite.
On peut penser que :
\, dt= \frac{(-1)^n n!}{(n+1)^{n+1}})
[edition] mes excuses pour l'orthographe. Il est tard...
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Déc 2006, 08:40
C'est ça, seul l'exposant de lnt bouge.
On voit mieux en posant
^qdt)
.
L'IPP que j'indiquais donne
d'où l'on tire
^qq!}{(p+1)^{q+1}})
.
En faisant p=q, on trouve la relation de nuage.
par sandrine_guillerme » 02 Déc 2006, 08:59
Oui moi je trouve que c'est correct en meme temps que joli.. :++: mais j'ai peut être d'autres questions comme celle là par exemple ..
en posant g=exp o f après avoir expliciter g et remarquer que que
=t^t)
montrer que
^{n-1}}{n^n})
Merci beaucoup d'avance .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
par yos » 02 Déc 2006, 09:30
, donc
=\sum_{n\geq 0}\frac{t^n(\ln t)^n}{n!}})
.
Il te reste à prendre l'intégrale des deux côtés et à justifier la permutation des symboles
et
.
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
par flaja » 02 Déc 2006, 09:34
ça n'aurait pas un rapport avec l'exercice précédent ?
 = \sum (t \ln t)^n / n!)
par sandrine_guillerme » 02 Déc 2006, 12:34
ah oué pour faire ceci il faut vérifier la convergence uniforme ..
oui ensuite on reste toujours avec notre fonction g mais cette fois ci je souhaite montrer que
\, dt = \sum_{i=0}^{+\infty} \int_{0}^{1} f_i(t)\, dt)
j'aime montrer la convergence normale donc il y a convergence uniforme mais pour montrer ceci je ne vois pas trop ..
à laide ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 02 Déc 2006, 13:11
Bonjour,
pour la convergence normale, tu peux montrer que
^n / n!)
converge normalement en majorant
)
sur [0;1]...
-
serge75
- Membre Relatif
- Messages: 432
- Enregistré le: 05 Avr 2006, 22:31
-
par serge75 » 02 Déc 2006, 15:45
oui ; voire même si on est fainéant par une constante K qui existe car t->tln(t) est continue sur le compact [0,1] (quitte à prolonger par continuité en 0).
par sandrine_guillerme » 02 Déc 2006, 15:48
j'ai remarquer que tu as toujours des raccourcis toi .. c'est bien .. merci à tout le monde d'ailleurs .
P.S: je laisse ce post ouvert au cas ou j'ai des question .
par sandrine_guillerme » 02 Déc 2006, 15:57
yos a écrit:C'est ça, seul l'exposant de lnt bouge.
On voit mieux en posant
.
L'IPP que j'indiquais donne
d'où l'on tire
.
En faisant p=q, on trouve la relation de nuage.
la j'ai une question .. pour l'intègrale que tu as posé la I_{p,q} il ne faut pas distinguer les cas ou i = 0 du cas i > 0 ? et et à quoi ça pourrait être égal I_{p,p} et I_{p,0} je suis peut être magniac je sais .. je suis navrée ..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
