Exo type oral CCP PSI(difficile)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
abel
- Membre Relatif
- Messages: 258
- Enregistré le: 17 Mar 2006, 17:59
-
 par abel » 20 Juin 2006, 16:29
par abel » 20 Juin 2006, 16:29
Bonjour,
Je seche sur un exo depuis un ptit moment donc je demande votre aide :
Il s'git de trouver les fonctions C0 de [0,1] dans R+ telles que :
 = \sum_{n=1}^{+\infty}\frac{f(x^{n})}{2^{n}})
Déjà les fonctions constantes conviennent et je pense que se sont les seules car je visualise ça comme une sorte de "moyenne" des f(x^n) vu que la somme des 1/2^n vaut 1...Du coup, f(x) doit etre "égale" à sa moyenne donc elle doit etre constante...enfin je pense
De meme j'ai trouvé que si f convient alors f+constante convient aussi donc on peut fixer une valeur particulière de f (genre f(0)=1) etc...)
Merci de votre aide.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Juin 2006, 17:02
par aviateurpilot » 20 Juin 2006, 17:02
je suis encor en terminal ,si j'ai pas fais de faute
voila ce que j'ai trouvé
-f(x^n)}{2^n}=0)
-
abel
- Membre Relatif
- Messages: 258
- Enregistré le: 17 Mar 2006, 17:59
-
 par abel » 20 Juin 2006, 17:08
par abel » 20 Juin 2006, 17:08
J'ai aussi obtenu ceci mais le pb c'est que l'on a aucune hypothese sur les variations de f (sinon si f etait croissante, on aurait tout de suite la conclusion).
Quelqu'un a une idée ??
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Juin 2006, 17:10
par aviateurpilot » 20 Juin 2006, 17:10
alors si f est strictement monotone sur un [0;r] avec 0alors quelque soit n les thermes de la somme que j'ai donné ont le meme signe si x appartien à [0;r]
f(x^{n+1})=f(x^n) sur [0;r] quelque soit n
donc f(x)=limf(x^n)=f(0)
donc f sera constante sur [0;r]
-
mathelot
 par mathelot » 20 Juin 2006, 22:10
par mathelot » 20 Juin 2006, 22:10

étant continue sur

est bornée et atteint ses bornes.
soit m son minimum et M son maximum.
quitte à changer

en
+m)
, on peut supposer que f atteint son minimum en x=0.
soit

tel que f atteint son maximum en

.
1er cas:
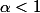
alors
=M=\sum_{k=1}^{+\infty}\frac{f(\alpha^{k})}{2^{k}})
d'où
=M)
or
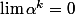
quand
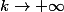
d'ou par continuité:
= \lim f(\alpha^{k})=M)
d'où
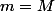
et la fonction f est constante.
2ème cas:
f atteint son minimum en

et son maximum en

.je n'ai pas su faire.
-
mathelot
 par mathelot » 21 Juin 2006, 09:39
par mathelot » 21 Juin 2006, 09:39
f est continue sur l'intervalle [0;1]. Donc f est bornée et f atteint son minimum m et son maximum M. si f n'est pas constante, quitte à remplacer f par la fonction

, on peut supposer que

, que m=0 et M=1.
j'ai pu conclure dans le cas particulier suivant: si f atteint son minimum en un point

et f atteint son maximum en un point

alors on a l'égalité:
=\sum_{k=1}^{+\infty}\frac{f(\alpha^{k})}{2^{k}} =0)
d'où:
=0)
comme
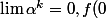=f(\lim \alpha^{k})=0=m.)
=\sum_{k=1}^{+\infty}\frac{f(\beta^{k})}{2^{k}}=M)
d'où:
=M)
comme
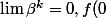=f(\lim \beta^{k})=M)
d'où m=f(0)=M et f est donc constante.
reste à traiter le cas où f atteint son maximum en x=1
ou le cas ou f atteint son minimum en x=1.
-
abel
- Membre Relatif
- Messages: 258
- Enregistré le: 17 Mar 2006, 17:59
-
 par abel » 21 Juin 2006, 10:19
par abel » 21 Juin 2006, 10:19
Salut, et merci de ta reponse par contre je n'ai pas compris ce passage de ton raisonnement :
=\sum_{k=1}^{+\infty}\frac{f(\beta^{k})}{2 ^{k}}=M)
d'où:
=M)
EDIT : Ah si en fait j'ai compris, merci beaucoup, je vais regarder les autres cas.
- Dans le cas où f est mini ou maxi pour x=1 on peut travailler sur un segment inclus dans [0,1] ne contenant pas 1, donc avec ton raisonnement, f sera constante sur tout compact ne contenant pas 1 et par continuité f(1) sera déterminé. Par contre je n'arrive pas bien a formaliser ceci...
-
mathelot
 par mathelot » 21 Juin 2006, 12:36
par mathelot » 21 Juin 2006, 12:36
abel a écrit:Dans le cas où f est mini ou maxi pour x=1 on peut travailler sur un segment inclus dans [0,1] ne contenant pas 1, donc avec ton raisonnement, f sera constante sur tout compact ne contenant pas 1 et par continuité f(1) sera déterminé. Par contre je n'arrive pas bien a formaliser ceci...
oui, d'après ta remarque, il est clair pour moi maintenant qu'il n'y a que les fonctions constantes qui vérifient l'équation.
-
mathelot
 par mathelot » 21 Juin 2006, 12:57
par mathelot » 21 Juin 2006, 12:57
je termine ton raisonnement.
supposons
=0=\min_{[0;1]} f)
et

d'où
=0=\min_{[0;x]} f)
Sur l'intervalle compact
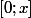
avec
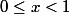
f atteint son maximum

. f est donc constante sur [0;x]
car
=m=M_{x})
donc

est constante sur
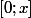
f est donc constante sur [0;1[ puis par continuité sur [0;1].
dans le cas où
=1=\max_{[0;1]}f)
, on traite de la même
façon en considérant

, le minimum de f sur [0;x].
je pense que le résultat est démontré.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 21 Juin 2006, 13:18
par tize » 21 Juin 2006, 13:18
BRAVO mathelot ! Joli
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
