Opérateurs compacts
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 03 Sep 2008, 15:19
par legeniedesalpages » 03 Sep 2008, 15:19
Bonjour,
je bloque sur ce problème:
Soient

et

des espaces vectoriels normés et

une application linéaire de

dans

.
Je ne vois pas comment procéder pour montrer que si
)
est finie, alors

est compacte.
Merci pour votre aide.
-
charif
- Membre Relatif
- Messages: 174
- Enregistré le: 30 Mar 2007, 19:32
-
 par charif » 03 Sep 2008, 15:23
par charif » 03 Sep 2008, 15:23
bs:
une application compacte .....????,,,
c'est nouveau !!!!!!!!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Sep 2008, 15:33
par Doraki » 03 Sep 2008, 15:33
Une boule fermée d'un evn de dimension finie est toujours compacte.
est-ce que T est continue ?
 par legeniedesalpages » 03 Sep 2008, 15:43
par legeniedesalpages » 03 Sep 2008, 15:43
Doraki a écrit:est-ce que T est continue ?
c'est pas dit dans l'énoncé.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 03 Sep 2008, 15:47
par Doraki » 03 Sep 2008, 15:47
Ben si c'est pas précisé tu peux pas faire grand chose.
N'importe quel opérateur non continu est un contre-exemple à ton exercice.
En supposant T continue, par contre le résultat est vrai et pas très dur à montrer.
-
charif
- Membre Relatif
- Messages: 174
- Enregistré le: 30 Mar 2007, 19:32
-
 par charif » 03 Sep 2008, 15:54
par charif » 03 Sep 2008, 15:54
[quote="legeniedesalpages"]Bonjour,
alors

est compacte.
c'est quoi une
application compacte??,,
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 03 Sep 2008, 16:01
par yos » 03 Sep 2008, 16:01
La continuité de f est parfois écrite par l'appartenance à L(E,F) avec un L en majuscule cursive.
 par legeniedesalpages » 04 Sep 2008, 09:53
par legeniedesalpages » 04 Sep 2008, 09:53
je cherche un exemple d'application linéaire continue non compacte. Il me semble que l'identité
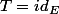
convient si

est un Banach de dimension infinie, en vertu du théorème de Riesz qui dit que les boules fermées ne sont pas compactes.
Enfin je dois montrer que
)
, l'ensemble des applications linéaires compactes de

dans

, est un sous-espace vectoriel fermé de
)
.
Donc j'ai montré que c'est un sous-espace, mais j'ai du mal pour montrer que
)
est fermé. :briques:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 04 Sep 2008, 11:19
par Doraki » 04 Sep 2008, 11:19
J'imagine que F est un espace de Banach et donc qu'il est complet ?
Ben tu prends une suite d'opérateurs compacts Tn qui converge vers T dans L(E,F), et une suite bornée (xk) d'éléments de E. Comme les Tn sont compacts, les suites Tn(xk) ont des valeurs d'adhérence dans F.
Tu dois alors montrer que la suite T(xk) aussi a une valeur d'adhérence dans F.
 par legeniedesalpages » 04 Sep 2008, 19:00
par legeniedesalpages » 04 Sep 2008, 19:00
ok ça devait être encore une erreur d'énoncé, du coup ça paraît plus facile, merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités