Opérateurs compacts
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 04 Mar 2017, 13:22
par Lostounet » 04 Mar 2017, 13:22
Bonjour,
Quelques questions pour comprendre ...
Si A est linéaire continu, on sait qu'il existe un unique adjoint A*.
Soit H un hilbert séparable et deux bases hilbertiennes
)
et
)
(il en existe car séparable)
C'est peut-être tout bête mais... pourquoi
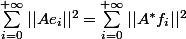
?
Et si on avait pris d'autres bases genre (en'), cela voudrait alors dire qu'avec l'adjoint on peut toujours se ramener à une même base (fn) non?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Mar 2017, 14:21
par zygomatique » 04 Mar 2017, 14:21
salut
pas bien clair ... l'énoncé est-il complet (comme H !!!) ?
mais il me semble que par définition :
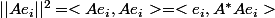
de même
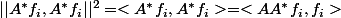
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Mar 2017, 18:29
par Ben314 » 04 Mar 2017, 18:29
Je comprend que dalle à ton truc : ton "
application linéaire continue A", elle va de quoi dans quoi ?
Si c'est de H dans H, le premier exemple qui me vient à l'esprit, c'est A=
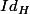
et la série
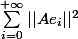
est grossièrement divergente (on somme que des 1...)
Et pour qu'une telle série converge, ben c'est clairement tout sauf "gratuit"...
Lostounet a écrit:Et si on avait pris d'autres bases genre (en'), cela voudrait alors dire qu'avec l'adjoint on peut toujours se ramener à une même base (fn) non?
Et ça je comprend même pas le sens que ça pourrait avoir : tu veut dire quoi par "
se ramener à" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Mar 2017, 19:05
par Ben314 » 04 Mar 2017, 19:05
En recherchant sur le net, j'ai fini par retrouver le nom que ça porte les opérateurs en question :
Définition : Si

est un Hilbert séparable on dit qu'une application linéaire
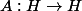
est
un opérateur de Hilbert-Schmidt lorsque qu'il existe une base Hilbertienne
_{n\geq 0})
telle que la série
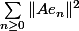
soit convergente.
Théorème : Si

est un opérateur de Hilbert-Schmidt alors il est continu et même compact, son adjoint
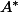
est aussi de Hilbert-Schmidt et
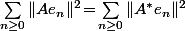
qui en fait ne dépend pas de la base Hilbertienne
_{n\geq 0})
.
Définition : On note
^{1/2})
.
Et c'est un bon exercice de chercher la preuve du théorème en question qui n'est pas super dure via l'égalité de Parseval.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 04 Mar 2017, 19:52
par Lostounet » 04 Mar 2017, 19:52
Ben314 a écrit:Je comprend que dalle à ton truc : ton "
application linéaire continue A", elle va de quoi dans quoi ?
Si c'est de H dans H, le premier exemple qui me vient à l'esprit, c'est A=
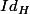
et la série
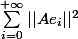
est grossièrement divergente (on somme que des 1...)
Et pour qu'une telle série converge, ben c'est clairement tout sauf "gratuit"...
Lostounet a écrit:Et si on avait pris d'autres bases genre (en'), cela voudrait alors dire qu'avec l'adjoint on peut toujours se ramener à une même base (fn) non?
Et ça je comprend même pas le sens que ça pourrait avoir : tu veut dire quoi par "
se ramener à" ?
Bonjour et merci de vos réponses...
Désolé, je n'ai pas pris le temps de bien définir le cadre de travail...
La série peut diverger mais il semble qu'il y ait une condition sur cette série (convergence) pour assurer la compacité de A.
Merci, je vais chercher du côté de Parseval
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Mar 2017, 20:55
par Ben314 » 04 Mar 2017, 20:55
Lostounet a écrit:La série peut diverger mais il semble qu'il y ait une condition sur cette série (convergence) pour assurer la compacité de A.
Oui, mais
ce n'est pas une C.N.S. : la série peut parfaitement diverger alors que l'opérateur est compact.
Sauf erreur, une C.N.S. pour qu'il soit compact, c'est que
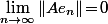
pour une base Hilbertiennes (<=> c'est vrai pour toutes les base Hilbertiennes) et c'est bien évidement strictement plus faible comme condition que la c.v. de la série
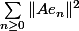
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
