Operateur non borné
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kingudamu
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Nov 2018, 14:49
-
par Kingudamu » 18 Avr 2020, 09:14
Bonjour,
Soit
l’opérateur de multiplication par
sur
)
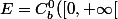(fcts
continues bornées sur
).
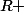
Quel est le domaine de
?
est-il un opérateur borné sur
?
Montrer que A est fermé et déterminer son adjoint et le domaine de l'adjoint.
soit f une fonction borné sur
,
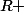
 = xf(x))
le domaine de
est
)
On se munit de la norme infinie/sup et on considère une fonction f tel que
(
)
par exemple))
on a
||_{\infty})
=
||_{\infty} \leq ||x||_{\infty})
qui ne peut pas être borné pour x dans E
Merci d'avance
-
GaBuZoMeu
- Habitué(e)
- Messages: 6120
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 18 Avr 2020, 09:41
Qui est
?
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 18 Avr 2020, 09:58
Salut,
GaBuZoMeu a écrit:Qui est
?
L'énoncé est incompréhensible, mais j'aurais tendance à penser que le 't', c'est la variable, c'est à dire que pour certaines fonctions
(à déterminer) l'élément
)
est défini par
(t)\!=\!t\!\times\!f(t))
.
Mais bon, c'est tout sauf une certitude . . .
Par contre la partie manquante d'énoncé où je n'ai pas d'idée, c'est celle concernant l'adjoint : je vois pas bien quoi prendre comme forme préhilbertienne "standard" sur E et ça me semble un peu étrange qu'il s'agisse de l'adjoint au sens du dual de E, vu que ce dual n'est pas tellement classique.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
par tournesol » 18 Avr 2020, 12:44
L'opérateur est précisé ligne 8 par Af(x)=xf(x)
-
Kingudamu
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Nov 2018, 14:49
-
par Kingudamu » 18 Avr 2020, 20:16
L'énoncé est:
Pour 2), j'ai pu trouvé un contre exemple avec
la norme L2 de f est 1
||_{2}^{2} = \int_{n}^{n+1} t^2 dt = \left[\frac{t^3}{3}\right]_{n}^{n+1} \geq n^2)
d'où
||}{||f||} \geq n \longrightarrow +\infty)
donc c'est pas bornée.
Pour la fermeture c'est direct, si on prend une suite
dans E,
on a directement que
et je trouve que
(auto-adjoint) car si on prend une fonction test v dans
})
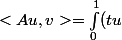vdt = \int_{0}^{1} u(t v)dt = <u,Av>)
ça me semble trop facile du coup j'ai un doute.
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 18 Avr 2020, 20:20
Perso, là où j'ai plus que des doutes, c'est sur le fait que la norme sur ton ensemble E soit la norme L2.
Selon toi, la fonction f constante égale à 1 sur [0,+oo[, elle est ou elle n'est pas dans E ?
Et la norme L2 de f, elle vaut combien ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Kingudamu
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Nov 2018, 14:49
-
par Kingudamu » 18 Avr 2020, 20:48
La norme L2 c'est moi qui l'ai choisi pour le contre exemple.
f = 1 est continue bornée sur [0,+oo[ donc elle est dans E.
Si f = 1 sur [0,+oo[ alors la norme L2 de f vaut +oo.
Mais au dessus j'ai pris f = la fonction indicatrice sur l’intervalle [n,n+1] inclus dans E
Je vais cherche un autre contre exemple.
-
Kingudamu
- Membre Naturel
- Messages: 16
- Enregistré le: 12 Nov 2018, 14:49
-
par Kingudamu » 18 Avr 2020, 23:58
Un autre contre exemple (?): on munit l'espace de la norme L1
 = \frac{e^{\frac{-t} {n}}}{n})
qui est bien une fonction continu borné sur E.
||_ 1 = \int_{0}^{+\infty} |f_n(t)| dt)
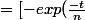]_{0}^{+\infty} = 1)
et
||_ 1 = \int_{0}^{+\infty} |t f_n(t)| dt = \int_{0}^{+\infty} t<br />\frac{exp{\frac{-t} {n}}}{n} dt)
en faisant une I.P.P (en dérivant le t et intégrant l'exp), on tombe sur
donc
||_1}{||f||_1} \geq n)
qui diverge lorsque n -> +oo
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 19 Avr 2020, 00:38
Kingudamu a écrit:Si f = 1 sur [0,+oo[ alors la norme L2 de f vaut +oo.
Deux "rappels" :
- Une
norme sur une espace vectoriel réel (ou complexe)
c'est, par définition, une application de
dans
.
- +oo n'est pas un réel.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
