Opérateur borné - analyse fonctionnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 09 Déc 2007, 19:37
par franz2b » 09 Déc 2007, 19:37
Salut a tous,
j'aimerai avoir de l'aide sur cet exercice:
Soit
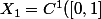)
muni de la norme
|)+max_{x \in [0,1]}(|f'(x)|))
Est ce que l'opérateur
 \to C([0,1]))
est borné.
Si oui, calculer sa norme.
merci beaucoup
 par legeniedesalpages » 09 Déc 2007, 20:38
par legeniedesalpages » 09 Déc 2007, 20:38
non c'est pas la norme sup, c'en est encore une autre.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 09 Déc 2007, 22:28
par ThSQ » 09 Déc 2007, 22:28
legeniedesalpages a écrit:non c'est pas la norme sup, c'en est encore une autre.
Laquelle ?
 par legeniedesalpages » 09 Déc 2007, 22:39
par legeniedesalpages » 09 Déc 2007, 22:39
ben franz l'a donné:
Soit
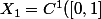)
muni de la norme
|)+max_{x \in [0,1]}(|f'(x)|))
je sais pas comment elle s'appelle, mais à la différence de la norme sup, elle prend en compte la variation de f.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 09 Déc 2007, 22:44
par ThSQ » 09 Déc 2007, 22:44
legeniedesalpages a écrit:ben franz l'a donné:
je sais pas comment elle s'appelle, mais à la différence de la norme sup, elle prend en compte la variation de f.
Ben non ça c'est la norme sur l'espace de départ. Mais à l'arrivée à savoir C([0;1]) ?????
 par legeniedesalpages » 09 Déc 2007, 22:48
par legeniedesalpages » 09 Déc 2007, 22:48
ah oui pardon, désolé pour ce quiproquo :hum:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 09 Déc 2007, 22:52
par ThSQ » 09 Déc 2007, 22:52
c pô grâf ...
Ca
doit être
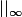
Au passage je me demande s'il y a des fonctions qui atteignent la norme.
 par busard_des_roseaux » 09 Déc 2007, 23:05
par busard_des_roseaux » 09 Déc 2007, 23:05
oui, on peut diviser les deux membres de l'inégalité par
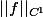
qui est un scalaire et le faire rentrer dans L().
||_C \leq 1)
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 09 Déc 2007, 23:07
par franz2b » 09 Déc 2007, 23:07
oui, la norme de depart n'est pas donnée dans l'exo, mais la norme infinie parait etre la plus naturelle.
J'etais sur un pb d'equicontinuité (qui me pose tj pb d'ailleur :) ), je vais dessuite regarder ce pb d'operateur borné et denorme...A+
je reviens vous dire si j'ai tout bien compris ..
 par busard_des_roseaux » 09 Déc 2007, 23:28
par busard_des_roseaux » 09 Déc 2007, 23:28
La norme de L est 1:
en effet:
| \leq 1)
On pose la suite de fonctions:
=\frac{sin(n\pi x)}{n \pi})
alors:
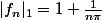
on pose
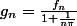
en regardant la suite
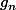
, on voit
 \geq \frac{1}{1+\frac{1}{n \pi}})
d'où:
|=1)
La norme est évidemment pas atteinte en un f sinon on aurait:
|max f|=0 et |max f'|=1
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 09 Déc 2007, 23:31
par franz2b » 09 Déc 2007, 23:31
Alors, j'ai pas tres bien saisi comment on arrive a l'inegalité:
\||_{C^1} \le \||f\||_{C^1})
\||_{C^1}=max(|L(f)(x)|)+max(|L(f')(x)|))
(ne serai-ce pas un sup d'ailleurs au lieu du max?.....)
enfin bref..
\||_{C^1}=max(|L(f)(x)|)+max(|L(f')(x)|)=max(|f'(x)|)+max(|f''(x)|) \le \||f\||_{C^1}+max(|f''(x)|))
et là plus rien......j'arrive pas a suivre.. :triste:
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 09 Déc 2007, 23:48
par franz2b » 09 Déc 2007, 23:48
Je pars de
\||}{\||f\||_{C^1}} ))
\||)
est elle bien celle que j'ai ecrite au dessus? :doute2:
 par busard_des_roseaux » 09 Déc 2007, 23:50
par busard_des_roseaux » 09 Déc 2007, 23:50
franz2b a écrit:Alors, j'ai pas tres bien saisi comment on arrive a l'inegalité:
\||_{C^1} \le \||f\||_{C^1})
l'opérateur L , qui n'est rien d'autre qu'une application (dont la
variableest une fonction) a pour ensemble d'arrivée
)
l'inégalité que tu as écrite n'a pas de sens. A remplacer par:
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 10 Déc 2007, 00:18
par franz2b » 10 Déc 2007, 00:18
busard_des_roseaux a écrit:l'opérateur L , qui n'est rien d'autre qu'une application (dont la
variableest une fonction) a pour ensemble d'arrivée
)
l'inégalité que tu as écrite n'a pas de sens. A remplacer par:
nickel busard!!
(x)|=f'(x))
Donc
\| \le \||f\||_{C^1})
Donc
\|}{\||f\||_{C^1}} \le 1)
l'opérateur est bien borné donc continu!!
Que ta nuit soit excellente Busard.....Merci infiniment
-
franz2b
- Membre Naturel
- Messages: 40
- Enregistré le: 10 Mai 2006, 15:04
-
 par franz2b » 10 Déc 2007, 01:10
par franz2b » 10 Déc 2007, 01:10
Pour ce qui est de la norme de L
dites moi si c'est bien ca:
=\frac{sin(n \pi x)}{n \pi})
=cos(n \pi x))
donc
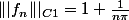
St
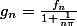
=>
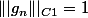
Donc
|=\frac{|f_n|}{1+\frac{1}{n \pi}} \le \frac{\||f_n\||_{C1}}{1+\frac{1}{n \pi}}=1 \le \|||L\|||) ccl
ccl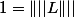
???
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités