salut:
je bloque sur cet exo, j'aimerais avoir un peu de l'aide :
E un C-espace vectoriel de dimension finie, u un endomorophisme de E tel que u^2 est diagonalisable
Mq u diagonalisable <==> ker(u)=ker(u^2).
en fait, c'est l'implication réciproque qui me crée un problème..
Merci d'avance;
Noyaux et diagonalisation
11 messages
- Page 1 sur 1
Le problème de ma méthode c'est si 0 est valeur propre de 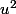 , le polynôme P n'a pas de terme constant et du coup Q a 0 comme racine double. On peut contourner ce problème en remplaçant
, le polynôme P n'a pas de terme constant et du coup Q a 0 comme racine double. On peut contourner ce problème en remplaçant 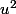 par
par  avec a convenable pour que 0 soit pas valeur propre.
avec a convenable pour que 0 soit pas valeur propre.
Ca donne :
u^2 diagonalisable.
 diagonalisable.
diagonalisable.
=0) avec P à racines simples non nulles.
avec P à racines simples non nulles.
=P(X^2+a))
Q(u)=0.
Q n'a que des racines simples.
U diagonalisable.
Ca donne :
u^2 diagonalisable.
Q(u)=0.
Q n'a que des racines simples.
U diagonalisable.
Rien à faire, mon truc est encore faux.
Essayons autrement.
Soit a une vp non nulle de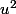 ,
,  l'espace propre associé. Puisque u commute avec
l'espace propre associé. Puisque u commute avec 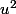 , il laisse stable
, il laisse stable  et sa restriction
et sa restriction 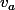 à
à  est annulée par
est annulée par 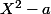 qui n'a que des racines simples, donc
qui n'a que des racines simples, donc 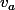 est diagonalisable.Si 0 est vp de
est diagonalisable.Si 0 est vp de 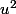 , on n'a pas de problème car
, on n'a pas de problème car  (égalité des sous-espaces propres).
(égalité des sous-espaces propres).
En recollant toutes les restrictions, on doit avoir u diagonalisable.
Essayons autrement.
Soit a une vp non nulle de
En recollant toutes les restrictions, on doit avoir u diagonalisable.
Je v essayé de reprendre ce qui a été dit.
L'endomorphisme u² est diagonalisable. Son polynome minimal est donc scindé à racines simples.
Ecrivons le:
=(X-\lambda_{1})\times \ldots \times (X-\lambda_{p}))
Ceci annule u²
Par conséquent le polynome
=(X^{2}-\lambda_{1}) \times \ldots \times (X^{2}-\lambda_{p})) est annulateur de u.
est annulateur de u.
On va distingué 2 cas
-Premier cas: 0 n'est pas valeur propre de u²
Comme on est dans C, soit une racine carrée de
une racine carrée de 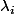 pour tout i entre 1 et p.
pour tout i entre 1 et p.
Le polynome Qu devient alors.
=(X-\mu_{1}) \times(X+\mu_{1}) \times\ldots \times (X-\mu_{p})\times (X+\mu_{p}))
Ce polynome est un polynome annulateur de u, scindé à racines simples donc u est diagonalisable.
- Deuxieme cas: 0 est valeur propre
Considerons la restruction de u à la somme des autres espaces propres de u² (ceux qui sont pas associés à la valeur propre 0).
Par le même raisonnement que le premier cas, cette restriction de u est diagonalisable. (Notons P le polynome annulateur de cette restriction de u)
Le probleme reste donc sur le sous espace propre associé à la valeur propre 0. (Autrement dit sur ker u²)
On sait que u² est diagonalisable donc que X² annule la restriction de u à ce sous espace propre.
Or ker u=ker u² donc X annule la restriction de u à ce sous espace propre.
Ainsi) est annulateur de u (il annule u sur tous les espaces propres de u² dont la somme forme l'espace tout entier).
est annulateur de u (il annule u sur tous les espaces propres de u² dont la somme forme l'espace tout entier).
Or ce polynome est scindé à racine simple.
u est diagonalisable.
Tout repose sur la propriété suivante:
Un endomorphisme u de E est diagonalisable ssi il existe un polynome annulateur de u scindé à racines simples.
(ssi son polynome minimal est scindé à racines simples)
puis aussi que un endo u de E est diago ssi E s'ecrit comme somme direct des sous espaces propres de u
L'endomorphisme u² est diagonalisable. Son polynome minimal est donc scindé à racines simples.
Ecrivons le:
Ceci annule u²
Par conséquent le polynome
On va distingué 2 cas
-Premier cas: 0 n'est pas valeur propre de u²
Comme on est dans C, soit
Le polynome Qu devient alors.
Ce polynome est un polynome annulateur de u, scindé à racines simples donc u est diagonalisable.
- Deuxieme cas: 0 est valeur propre
Considerons la restruction de u à la somme des autres espaces propres de u² (ceux qui sont pas associés à la valeur propre 0).
Par le même raisonnement que le premier cas, cette restriction de u est diagonalisable. (Notons P le polynome annulateur de cette restriction de u)
Le probleme reste donc sur le sous espace propre associé à la valeur propre 0. (Autrement dit sur ker u²)
On sait que u² est diagonalisable donc que X² annule la restriction de u à ce sous espace propre.
Or ker u=ker u² donc X annule la restriction de u à ce sous espace propre.
Ainsi
Or ce polynome est scindé à racine simple.
u est diagonalisable.
Tout repose sur la propriété suivante:
Un endomorphisme u de E est diagonalisable ssi il existe un polynome annulateur de u scindé à racines simples.
(ssi son polynome minimal est scindé à racines simples)
puis aussi que un endo u de E est diago ssi E s'ecrit comme somme direct des sous espaces propres de u
Antho a tout dit je pense. Moi j'avais des problèmes de connexion.
Tu as donc où
où ) . La restriction de u à chaque
. La restriction de u à chaque  est diagonalisable donc on peut prendre une base
est diagonalisable donc on peut prendre une base 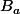 de chaque
de chaque  dans laquelle la matrice de
dans laquelle la matrice de  est diagonale. En posant
est diagonale. En posant  , on a une base
, on a une base  de E dans laquelle la matrice de u est diagonale.
de E dans laquelle la matrice de u est diagonale.
Mohamed a écrit:si toutes les restrictions sont diagonalisables, pourquoi u sera aussi diagonalisable?
Tu as donc
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
